题目内容
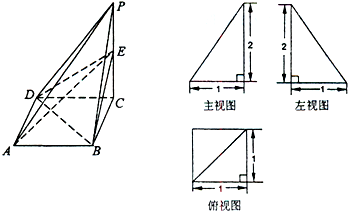
已知四棱锥P-ABCD及其三视图如下图所示,E是侧棱PC上的动点.
(Ⅰ)求四棱锥P-ABCD的体积;
(Ⅱ)不论点E在何位置,是否都有BD⊥AE?试证明你的结论;
(Ⅲ)若点E为PC的中点,求二面角D-AE-B的大小.
(Ⅰ)求四棱锥P-ABCD的体积;
(Ⅱ)不论点E在何位置,是否都有BD⊥AE?试证明你的结论;
(Ⅲ)若点E为PC的中点,求二面角D-AE-B的大小.

考点:二面角的平面角及求法,棱柱、棱锥、棱台的体积
专题:空间位置关系与距离,空间角
分析:(I)由三视图知PC⊥面ABCD,ABCD为正方形,且PC=2,AB=BC=1,由此能求出四棱锥P-ABCD的体积.
(II)不论点E在何位置,都有BD⊥AE.由已知得PC⊥BD,从而BD⊥面ACE,由此能证明BD⊥AE.
(III)连接AC,交BD于O.由对称性,二面角D-AE-B是二面角O-AE-B的2倍,设θ为二面角O-AE-B的平面角.注意到B在面ACE上的射影为O,由cosθ=
=
,能求出二面角D-AE-B的大小.
(II)不论点E在何位置,都有BD⊥AE.由已知得PC⊥BD,从而BD⊥面ACE,由此能证明BD⊥AE.
(III)连接AC,交BD于O.由对称性,二面角D-AE-B是二面角O-AE-B的2倍,设θ为二面角O-AE-B的平面角.注意到B在面ACE上的射影为O,由cosθ=
| S△AOE |
| S△ABE |
| 1 |
| 2 |
解答:
解:(I)由三视图知PC⊥面ABCD,
ABCD为正方形,且PC=2,AB=BC=1,
∴VP-ABCD=
SABCD×PC=
×12×2=
.(4分)
(II)不论点E在何位置,都有BD⊥AE.
证明如下: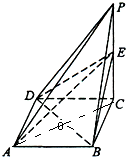
∵PC⊥面ABCD,BD?面ABCD,∴PC⊥BD
而BD⊥AC,AC∩AE=A,∴BD⊥面ACE,
而AE?面ACE,
∴BD⊥AE.(7分)
(III)连接AC,交BD于O.
由对称性,二面角D-AE-B是二面角O-AE-B的2倍,
设θ为二面角O-AE-B的平面角.
注意到B在面ACE上的射影为O,
S△AOE=
S△ACE=
×
×
=
,
S△ABE=
AB×BE=
,
∴cosθ=
=
,
∴θ=60°∴二面角D-AE-B是120°.(12分)
ABCD为正方形,且PC=2,AB=BC=1,
∴VP-ABCD=
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
(II)不论点E在何位置,都有BD⊥AE.
证明如下:

∵PC⊥面ABCD,BD?面ABCD,∴PC⊥BD
而BD⊥AC,AC∩AE=A,∴BD⊥面ACE,
而AE?面ACE,
∴BD⊥AE.(7分)
(III)连接AC,交BD于O.
由对称性,二面角D-AE-B是二面角O-AE-B的2倍,
设θ为二面角O-AE-B的平面角.
注意到B在面ACE上的射影为O,
S△AOE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| ||
| 4 |
S△ABE=
| 1 |
| 2 |
| ||
| 2 |
∴cosθ=
| S△AOE |
| S△ABE |
| 1 |
| 2 |
∴θ=60°∴二面角D-AE-B是120°.(12分)
点评:本试题主要考查了立体几何中的线面的垂直,以及二面角的求解的综合运用.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案
相关题目
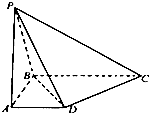 如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,∠ABC=90°,AD∥BC,AD=1,BC=2,又PB=1,∠PBC=120°,AB⊥PC,直线AB与直线PD所成的角为60°.
如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,∠ABC=90°,AD∥BC,AD=1,BC=2,又PB=1,∠PBC=120°,AB⊥PC,直线AB与直线PD所成的角为60°.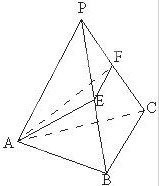 如图,设正三棱锥P-ABC的侧棱长为1,∠APB=30°,E、F分别是BP、CP上的一点,求△AEF周长的最小值.
如图,设正三棱锥P-ABC的侧棱长为1,∠APB=30°,E、F分别是BP、CP上的一点,求△AEF周长的最小值.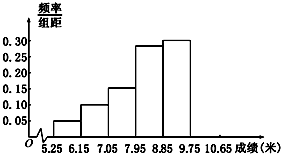 某市为了了解今年高中毕业生的体能状况,从本市某校高中毕业班中抽取一个班进行铅球测试,成绩在8.0米(精确到0.1米)以上的为合格.把所得数据进行整理后,分成6组画出频率分布直方图的一部分(如图),已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30,第6小组的频数是7.
某市为了了解今年高中毕业生的体能状况,从本市某校高中毕业班中抽取一个班进行铅球测试,成绩在8.0米(精确到0.1米)以上的为合格.把所得数据进行整理后,分成6组画出频率分布直方图的一部分(如图),已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30,第6小组的频数是7.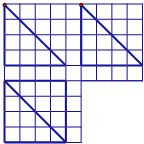 如图在边长为1的正方形网格中用粗线画出了某个多面体的三视图,则该多面体的外接球的体积为
如图在边长为1的正方形网格中用粗线画出了某个多面体的三视图,则该多面体的外接球的体积为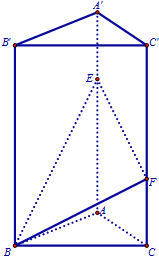 已知三棱柱ABC-A′B′C′中,面BCC′B′⊥底面ABC,BB′⊥AC,底面ABC是边长为2的等边三角形,AA′=3,E,F分别在棱AA′,CC′上,且AE=C′F=2.
已知三棱柱ABC-A′B′C′中,面BCC′B′⊥底面ABC,BB′⊥AC,底面ABC是边长为2的等边三角形,AA′=3,E,F分别在棱AA′,CC′上,且AE=C′F=2.