题目内容
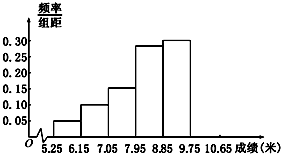某市为了了解今年高中毕业生的体能状况，从本市某校高中毕业班中抽取一个班进行铅球测试，成绩在8.0米（精确到0.1米）以上的为合格．把所得数据进行整理后，分成6组画出频率分布直方图的一部分（如图），已知从左到右前5个小组的频率分别为0.04，0.10，0.14，0.28，0.30，第6小组的频数是7．（1）求这次铅球测试成绩合格的人数；
（2）用此次测试结果估计全市毕业生的情况．若从今年的高中毕业生中随机抽取两名，记X表示两人中成绩不合格的人数，求X的分布列及数学期望．
考点：离散型随机变量及其分布列,离散型随机变量的期望与方差
专题：概率与统计
分析：（1）由频率分布直方图求出第6小组的频率，由此能求出此次测试总人数，由此能求出这次铅球测试成绩合格的人数．
（2）X=0，1，2，X～B（2，
），由此能求出X的分布列及数学期望．
（2）X=0，1，2，X～B（2，
| 7 |
| 25 |
解答：
解：（1）第6小组的频率为1-（0.04+0.10+0.14+0.28+0.30）=0.14，
∴此次测试总人数为
=50（人）．…（2分）
∴第4、5、6组成绩均合格，人数为（0.28+0.30+0.14）×50=36（人）…（5分）
（2）X=0，1，2，此次测试中成绩不合格的概率为
=
，…（6分）
∴X～B（2，
）．…（7分）
P（X=0）=(
)2=
，
P（X=1）=
(
)(
)=
，
P（X=2）=(
)2=
，…（10分）
所求分布列是：
EX=0×
+1×
+2×
=
．…（12分）
∴此次测试总人数为
| 7 |
| 0.14 |
∴第4、5、6组成绩均合格，人数为（0.28+0.30+0.14）×50=36（人）…（5分）
（2）X=0，1，2，此次测试中成绩不合格的概率为
| 14 |
| 50 |
| 7 |
| 25 |
∴X～B（2，
| 7 |
| 25 |
P（X=0）=(
| 18 |
| 25 |
| 324 |
| 625 |
P（X=1）=
| C | 1 2 |
| 7 |
| 25 |
| 18 |
| 25 |
| 252 |
| 625 |
P（X=2）=(
| 7 |
| 25 |
| 49 |
| 625 |
所求分布列是：
| X | 0 | 1 | 2 | ||||||
| P |
|
|
|
| 324 |
| 625 |
| 252 |
| 625 |
| 49 |
| 625 |
| 14 |
| 25 |
点评：本题考查频率分布直方图的应用，考查离散型随机变量的分布列和数学期望的求法，解题时要认真审题，注意二项分布的性质的合理运用．
练习册系列答案
相关题目
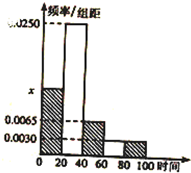某公司对夏季室外工作人员规定如下：当气温超过35℃时，室外连续工作时间严禁超过100分钟；不少于60分钟的，公司给予适当补助．随机抽取部分工人调查其高温室外连续工作时间（单位：分钟），并将所得数据绘制成频率分布直方图（如图），其中工作时间范围是[0，100]，样本数据分组为[0，20），[20，40），[40，60），[60，80），[80，100]．
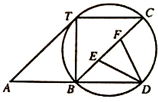如图，⊙O过平行四边形ABCT的三个顶点B，C，T，且与AT相切，交AB的延长线于点D．