题目内容
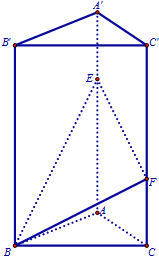 已知三棱柱ABC-A′B′C′中,面BCC′B′⊥底面ABC,BB′⊥AC,底面ABC是边长为2的等边三角形,AA′=3,E,F分别在棱AA′,CC′上,且AE=C′F=2.
已知三棱柱ABC-A′B′C′中,面BCC′B′⊥底面ABC,BB′⊥AC,底面ABC是边长为2的等边三角形,AA′=3,E,F分别在棱AA′,CC′上,且AE=C′F=2.(Ⅰ)求证:BB′⊥底面ABC;
(Ⅱ)在棱A′B′上找一点M,使得C′M∥面BEF,并给出证明.
考点:直线与平面垂直的判定,直线与平面平行的判定
专题:证明题,空间位置关系与距离
分析:(Ⅰ)取BC中点O,先证AO⊥BC,再由面面垂直的性质定理证得AO⊥面BCC'B',再由线面垂直的判定定理即可得证;
(Ⅱ) 显然M不是A',B',当M为A'B'的中点,使得C'M∥面BEF,可通过线面平行的判断定理,即可证得.
(Ⅱ) 显然M不是A',B',当M为A'B'的中点,使得C'M∥面BEF,可通过线面平行的判断定理,即可证得.
解答:
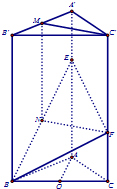 (Ⅰ)证明:取BC中点O,因为三角形ABC是等边三角形,所以AO⊥BC,
(Ⅰ)证明:取BC中点O,因为三角形ABC是等边三角形,所以AO⊥BC,
又因为面BCC'B'⊥底面ABC,AO?面ABC,面BCC'B'∩面ABC=BC,
所以AO⊥面BCC'B',又BB'?面BCC'B',
所以AO⊥BB'.又BB'⊥AC,AO∩AC=A,AO?面ABC,AC?面ABC,
所以BB'⊥底面ABC.
(Ⅱ) 显然M不是A',B',当M为A'B'的中点,使得C'M∥面BEF.
证明:过M作MN∥AA'交BE于N,则N为中点,
则MN=
(A'E+B'B)=2,则MN=C'F,MN∥C'F,
所以四边形C'MNF为平行四边形,所以C'M∥FN,
C'M?平面BEF,NF?平面BEF,所以C'M∥面BEF.
 (Ⅰ)证明:取BC中点O,因为三角形ABC是等边三角形,所以AO⊥BC,
(Ⅰ)证明:取BC中点O,因为三角形ABC是等边三角形,所以AO⊥BC,又因为面BCC'B'⊥底面ABC,AO?面ABC,面BCC'B'∩面ABC=BC,
所以AO⊥面BCC'B',又BB'?面BCC'B',
所以AO⊥BB'.又BB'⊥AC,AO∩AC=A,AO?面ABC,AC?面ABC,
所以BB'⊥底面ABC.
(Ⅱ) 显然M不是A',B',当M为A'B'的中点,使得C'M∥面BEF.
证明:过M作MN∥AA'交BE于N,则N为中点,
则MN=
| 1 |
| 2 |
所以四边形C'MNF为平行四边形,所以C'M∥FN,
C'M?平面BEF,NF?平面BEF,所以C'M∥面BEF.
点评:本题考查线面平行和垂直的判定和性质,以及面面垂直的性质定理,考查逻辑推理能力,属于中档题.

练习册系列答案
相关题目
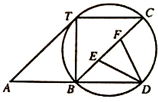 如图,⊙O过平行四边形ABCT的三个顶点B,C,T,且与AT相切,交AB的延长线于点D.
如图,⊙O过平行四边形ABCT的三个顶点B,C,T,且与AT相切,交AB的延长线于点D. 函数f(x)=Asin(ωx+φ)(A>0,ω>0,-
函数f(x)=Asin(ωx+φ)(A>0,ω>0,-