题目内容
求双曲线16x2-9y2=-144的实轴长、焦点坐标、离心率、渐近线方程、顶点坐标．
考点：双曲线的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：双曲线16x2-9y2=-144可化为
-
=1，可得a=4，b=3，c=5，从而可求双曲线的实轴长、焦点坐标、离心率、渐近线方程、顶点坐标．
| y2 |
| 16 |
| x2 |
| 9 |
解答：
解：双曲线16x2-9y2=-144可化为
-
=1，
所以a=4，b=3，c=5，
所以，实轴长为8，焦点坐标为（0，5）和（0，-5），
离心率e=
=
，渐近线方程为y=±
x，顶点坐标（0，±4）．
| y2 |
| 16 |
| x2 |
| 9 |
所以a=4，b=3，c=5，
所以，实轴长为8，焦点坐标为（0，5）和（0，-5），
离心率e=
| c |
| a |
| 5 |
| 4 |
| 4 |
| 3 |
点评：本题考查双曲线的标准方程，考查双曲线的几何性质，确定双曲线的几何量是关键．
练习册系列答案
名校通行证有效作业系列答案
相关题目
若点（m，n）在圆C：x2+y2=4的圆外，则直线l：mx+ny=4与圆C的关系是（ ）
| A、相离 | B、相切 |
| C、相交 | D、由m、n决定 |
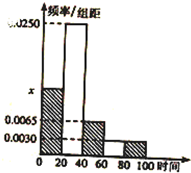某公司对夏季室外工作人员规定如下：当气温超过35℃时，室外连续工作时间严禁超过100分钟；不少于60分钟的，公司给予适当补助．随机抽取部分工人调查其高温室外连续工作时间（单位：分钟），并将所得数据绘制成频率分布直方图（如图），其中工作时间范围是[0，100]，样本数据分组为[0，20），[20，40），[40，60），[60，80），[80，100]．