题目内容
已知函数f(x)=xlnx,g(x)=-
x2+
x-
(Ⅰ)求f(x)在[t,t+1](0<t<
)上的最小值;
(Ⅱ)在函数f(x)与g(x)的公共定义域内f(x)的图象在g(x)图象的上方,求实数a的范围;
(Ⅲ)a=2时,曲线h(x)=
-2g(x)的图象上是否存在两点A,B,使
∥m(设线段AB的中点横坐标为x0,函数h(x)在x=x0处的切线的方向向量为m)?若存在,求出直线AB的方程,若不存在,请说明理由.
| 1 |
| 2 |
| a |
| 2 |
| 3 |
| 2 |
(Ⅰ)求f(x)在[t,t+1](0<t<
| 1 |
| e |
(Ⅱ)在函数f(x)与g(x)的公共定义域内f(x)的图象在g(x)图象的上方,求实数a的范围;
(Ⅲ)a=2时,曲线h(x)=
| f(x) |
| x |
| AB |
考点:利用导数研究函数的单调性,利用导数求闭区间上函数的最值
专题:计算题,压轴题,函数的性质及应用,导数的综合应用
分析:(Ⅰ)求导f′(x)=lnx+1;由导数确定函数的单调性,从而求最小值;
(Ⅱ)先求出函数f(x)与g(x)的公共定义域为(0,+∞);再化题意为x∈(0,+∞)时,f(x)-g(x)>0恒成立;从而化为a<2lnx+x+
,再记m(x)=2lnx+x+
,从而转化为函数的最值问题;
(Ⅲ)当a=2时,化简h(x)=
-2g(x)=lnx+x2-2x+3,从而假设存在两点A(x1,y1),B(x2,y2),(0<x1<x2)满足题意,即h′(x0)=
,可化为
=
;设
=z,则0<z<1;从而化为lnz=
;再令y=lnz-
,从而转化为是否有零点即可.
(Ⅱ)先求出函数f(x)与g(x)的公共定义域为(0,+∞);再化题意为x∈(0,+∞)时,f(x)-g(x)>0恒成立;从而化为a<2lnx+x+
| 3 |
| x |
| 3 |
| x |
(Ⅲ)当a=2时,化简h(x)=
| f(x) |
| x |
| h(x1)-h(x2) |
| x1-x2 |
| 2 |
| x1+x2 |
ln
| ||
| x1-x2 |
| x1 |
| x2 |
| 2(z-1) |
| 1+z |
| 2(z-1) |
| 1+z |
解答:
解:(Ⅰ)f′(x)=lnx+1;
则当x∈(0,
)时,f′(x)<0,当x∈(
,+∞)时,f′(x)>0,
f(x)在(0,
)上单调递减,在(
,+∞)上单调递增;
又∵0<t<
,
∴fmin(x)=f(
)=-
;
(Ⅱ)函数f(x)与g(x)的公共定义域为(0,+∞);
由题意知,x∈(0,+∞)时,f(x)-g(x)>0恒成立;
即xlnx+
x2-
x+
>0恒成立,
即a<2lnx+x+
,
记m(x)=2lnx+x+
,
则m′(x)=
;
故m(x)在(0,1)上为减函数,在(1,+∞)上为增函数;
故mmin(x)=m(1)=4;
故a<4;
(Ⅲ)a=2时,h(x)=
-2g(x)=lnx+x2-2x+3,
若存在两点A(x1,y1),B(x2,y2),(0<x1<x2)满足题意,
即h′(x0)=
,
即
+x1+x2-2=
+x1+x2-2;
故
=
;
设
=z,则0<z<1;
上式可化为lnz=
;
令y=lnz-
,
则y′=
-
=
>0;
故y在(0,1]上是增函数,ymax=0;
∴lnz-
<0;
故lnz=
不成立;
∴不存在满足题意的两点A,B.
则当x∈(0,
| 1 |
| e |
| 1 |
| e |
f(x)在(0,
| 1 |
| e |
| 1 |
| e |
又∵0<t<
| 1 |
| e |
∴fmin(x)=f(
| 1 |
| e |
| 1 |
| e |
(Ⅱ)函数f(x)与g(x)的公共定义域为(0,+∞);
由题意知,x∈(0,+∞)时,f(x)-g(x)>0恒成立;
即xlnx+
| 1 |
| 2 |
| a |
| 2 |
| 3 |
| 2 |
即a<2lnx+x+
| 3 |
| x |
记m(x)=2lnx+x+
| 3 |
| x |
则m′(x)=
| (x+3)(x-1) |
| x2 |
故m(x)在(0,1)上为减函数,在(1,+∞)上为增函数;
故mmin(x)=m(1)=4;
故a<4;
(Ⅲ)a=2时,h(x)=
| f(x) |
| x |
若存在两点A(x1,y1),B(x2,y2),(0<x1<x2)满足题意,
即h′(x0)=
| h(x1)-h(x2) |
| x1-x2 |
即
| 2 |
| x1+x2 |
ln
| ||
| x1-x2 |
故
| 2 |
| x1+x2 |
ln
| ||
| x1-x2 |
设
| x1 |
| x2 |
上式可化为lnz=
| 2(z-1) |
| 1+z |
令y=lnz-
| 2(z-1) |
| 1+z |
则y′=
| 1 |
| z |
| 4 |
| (z+1)2 |
| (z-1)2 |
| z(z+1)2 |
故y在(0,1]上是增函数,ymax=0;
∴lnz-
| 2(z-1) |
| 1+z |
故lnz=
| 2(z-1) |
| 1+z |
∴不存在满足题意的两点A,B.
点评:本题考查了导数的综合应用及恒成立问题,同时考查了换元法的应用,化简与运算也很困难,属于难题.

练习册系列答案
相关题目
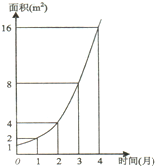 近几年,每年11月初,黄浦江上漂浮在大片的水葫芦,严重影响了黄浦江的水利、水质、航运和市容景观.为了解决这个环境问题,科研人员进行科研攻关.如图是科研人员在实验室池塘中观察水葫芦的面积与时间的函数关系图象.假设其函数关系为指数函数,并给出下列说法:
近几年,每年11月初,黄浦江上漂浮在大片的水葫芦,严重影响了黄浦江的水利、水质、航运和市容景观.为了解决这个环境问题,科研人员进行科研攻关.如图是科研人员在实验室池塘中观察水葫芦的面积与时间的函数关系图象.假设其函数关系为指数函数,并给出下列说法:
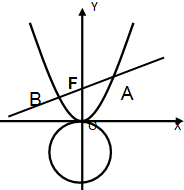 已知抛物线C:x2=4y,过焦点F的直线l与抛物线交于A,B两点(A在第一象限).
已知抛物线C:x2=4y,过焦点F的直线l与抛物线交于A,B两点(A在第一象限).