Question

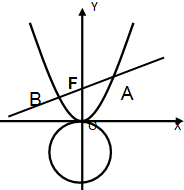已知抛物线C：x²=4y，过焦点F的直线l与抛物线交于A，B两点（A在第一象限）．
（Ⅰ）当S_△OFA=2S_△OFB时，求直线l的方程；
（Ⅱ）过点A（2t，t²）作抛物线C的切线l₁与圆x²+（y+1）²=1交于不同的两点M，N，设F到l₁的距离为d，求

|MN|

d

的取值范围．

Answer 1

考点：抛物线的简单性质

专题：圆锥曲线的定义、性质与方程

分析：（1）由S_△OFA=2S_△OFB，可得|AF|=2|FB|．设A(x1，

x 2 1

4

)，B(x2，

x 2 2

4

)，利用

x1=-2x2 x 2 1 4 +1=2( x 2 2 4 +1)

，解出即可；
（2）由于y=

x2

4

，因此y′=

1

2

x，可得切线l₁的方程为y-t²=t（x-2t），圆心（0，-1）到l₁的距离为d₁=

|1-t2|

t2+1

，且d₁＜1，故0＜t²＜3．则|MN|=2

1- d 2 1

=2|t|

3-t2 t2+1

，点F到l₁的距离d=

t2+1

，

|MN|

d

=2

3t2-t4 t4+2t2+1

，通过换元利用基本不等式的性质即可得出．

解答： 解：（1）∵S_△OFA=2S_△OFB，∴|AF|=2|FB|．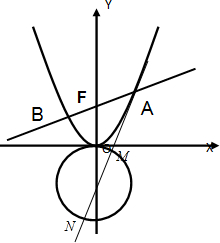
设A(x1，

x 2 1

4

)，B(x2，

x 2 2

4

)，则

x1=-2x2 x 2 1 4 +1=2( x 2 2 4 +1)

，
故

x

2 2

=2，
∴A(2

2

，2)．
因此直线l的方程为y=

2

4

x+1．
（2）由于y=

x2

4

，因此y′=

1

2

x，
故切线l₁的方程为y-t²=t（x-2t），
化简得tx-y-t²=0，
则圆心（0，-1）到l₁的距离为d₁=

|1-t2|

t2+1

，且d₁＜1，故0＜t²＜3．
则|MN|=2

1- d 2 1

=2|t|

3-t2 t2+1

，
则点F到l₁的距离d=

t2+1

，
则

|MN|

d

=2

3t2-t4 t4+2t2+1

，
令z=

3t2-t4

t4+2t2+1

=-1+

5t2+1

t2+2t2+1

=-1+

25m

m2+8m+16

，（m=5t²+1∈（1，16）．
则z=-1+

25

m+ 16 m +8

∈(0，

9

16

)，
故

|MN|

d

∈(0，

3

2

]．

点评：本题考查了抛物线的标准方程及其性质、直线与抛物线相交与相切问题、导数的几何意义、点到直线的距离公式、基本不等式的性质，考查了推理能力与计算能力，属于中档题．