题目内容
l是平面α外一条直线，过l作平面β，使α∥β，这样的β（ ）
| A、只能作一个 |
| B、至少可以做一个 |
| C、不存在 |
| D、至多可以作一个 |
考点：直线与平面平行的判定
专题：证明题,空间位置关系与距离
分析：由平面与平面平行的性质得这样的平面β有且只有1个．
解答：
解：当a∥α时，过a作平面β，使得β∥α，
由平面与平面平行的性质得：
这样的平面β有且只有1个．
a与α相交时，设平面为β，a与α交点为P，
根据题意P∈β，P∈α，则α∩β=l且P∈l，这与α∥β矛盾，
∴这样的β不存在．
综上所述，过平面α外一条直线a与α平行的平面的个数为至多1个．
故选：D．
由平面与平面平行的性质得：
这样的平面β有且只有1个．
a与α相交时，设平面为β，a与α交点为P，
根据题意P∈β，P∈α，则α∩β=l且P∈l，这与α∥β矛盾，
∴这样的β不存在．
综上所述，过平面α外一条直线a与α平行的平面的个数为至多1个．
故选：D．
点评：本题考查满足条件的平面的个数的求法，是基础题，解题时要注意空间思维能力的培养．
练习册系列答案
全能测控期末小状元系列答案
智趣暑假温故知新系列答案
相关题目
在△ABC中，角A，B，C的对边分别是a，b，c，若（a2+c2-b2）tanB=
ac，则角B的值为（ ）
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知m，n为异面直线，m?平面α，n?平面β，α∩β=l，则直线l（ ）
| A、与m，n都相交 |
| B、与m，n都不相交 |
| C、与m，n中至少一条相交 |
| D、至多与m，n中的一条相交 |
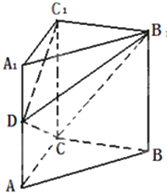如图，在直三棱柱ABC-A1B1C1中，∠ACB=90°，2AC=AA1=BC=2，D为棱AA1上的点．