题目内容
设偶函数f(x)的定义域为R,当x∈[0,+∞)时,f(x)是增函数,则f(-2),f(1),f(-3)的大小关系是( )
| A、f(1)>f(-3)>f(-2) |
| B、f(1)>f(-2)>f(-3) |
| C、f(1)<f(-3)<f(-2) |
| D、f(1)<f(-2)<f(-3) |
考点:函数单调性的性质,函数奇偶性的性质
专题:函数的性质及应用
分析:先利用偶函数的性质,将函数值转化到同一单调区间[0,+∞)上,然后比较大小.
解答:
解:因为f(x)是偶函数,所以f(-3)=f(3),f(-2)=f(2).
又因为函数f(x)在[0,+∞)上是增函数,
故f(3)>f(2)>f(1).
即f(-3)>f(-2)>f(1).
故选D
又因为函数f(x)在[0,+∞)上是增函数,
故f(3)>f(2)>f(1).
即f(-3)>f(-2)>f(1).
故选D
点评:本题考查了函数的单调性在比较函数值大小中的应用,要注意结合其它性质考查时,一般先将不同区间上的函数值转化到同一单调区间上再比较大小.

练习册系列答案
相关题目
空间直角坐标系中A(1,2,3),B(-1,0,5),C(3,0,4),D(4,1,3),则直线AB与CD的位置关系是( )
| A、平行 | B、垂直 |
| C、相交但不垂直 | D、无法确定 |
设a=log
4,b=3
,c=(
)0.4,则有( )
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 5 |
| A、a<b<c |
| B、a<c<b |
| C、c<a<b |
| D、c<b<a |
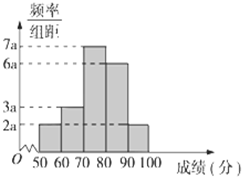 某校为了了解学生的数学学习情况,以5%的比例随机抽取20位学生,根据他们的期中考试数学成绩作出频率分布直方图如右图所示,其中成绩分组区间是:[50,60)、[60,70)、[70,80)、[80,90)、[90,100),
某校为了了解学生的数学学习情况,以5%的比例随机抽取20位学生,根据他们的期中考试数学成绩作出频率分布直方图如右图所示,其中成绩分组区间是:[50,60)、[60,70)、[70,80)、[80,90)、[90,100),