题目内容
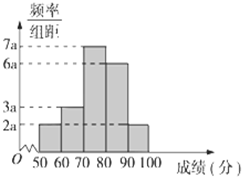 某校为了了解学生的数学学习情况,以5%的比例随机抽取20位学生,根据他们的期中考试数学成绩作出频率分布直方图如右图所示,其中成绩分组区间是:[50,60)、[60,70)、[70,80)、[80,90)、[90,100),
某校为了了解学生的数学学习情况,以5%的比例随机抽取20位学生,根据他们的期中考试数学成绩作出频率分布直方图如右图所示,其中成绩分组区间是:[50,60)、[60,70)、[70,80)、[80,90)、[90,100),(Ⅰ)求图中a的值,并根据频率分布直方图估计该校成绩落在[50,60)中的学生人数;
(Ⅱ)从样本中成绩在[50,70)的学生中人任选2人,求这2人的成绩都在[60,70)中的概率.
考点:频率分布直方图,古典概型及其概率计算公式
专题:概率与统计
分析:(I)根据频率和为1,求出a的值,再根据频率、频数与样本容量的关系求出对应的频数;
(Ⅱ)求出成绩在[50,60)与[60,70)范围内人数,计算从5人选2人的基本事件数,求出对应的概率即可.
(Ⅱ)求出成绩在[50,60)与[60,70)范围内人数,计算从5人选2人的基本事件数,求出对应的概率即可.
解答:
解:(I)由题知组距为10,频率和为1,
∴(2a+2a+3a+6a+7a)×10=1,
解得a=0.005;…(3分)
该校总人数为20÷5%=400,
由图知,落在[50,60)的频率为2a×10=0.1,
由此估计该范围内的人数为400×0.1=40; (6分)
(Ⅱ)记[50,60)范围内的有2人,[60,70)范围内的有3人,
从5人选2人共有10种情况,且每种情况等可能出现,
其中2人成绩都在[60,70)范围内的有3种情况,
∴所求概率为P=
.(12分)
∴(2a+2a+3a+6a+7a)×10=1,
解得a=0.005;…(3分)
该校总人数为20÷5%=400,
由图知,落在[50,60)的频率为2a×10=0.1,
由此估计该范围内的人数为400×0.1=40; (6分)
(Ⅱ)记[50,60)范围内的有2人,[60,70)范围内的有3人,
从5人选2人共有10种情况,且每种情况等可能出现,
其中2人成绩都在[60,70)范围内的有3种情况,
∴所求概率为P=
| 3 |
| 10 |
点评:本题考查了概率与统计的应用问题,解题时应根据频率和等于1,结合频率、频数与样本容量的关系,进行解答,是基础题.

练习册系列答案
相关题目
设偶函数f(x)的定义域为R,当x∈[0,+∞)时,f(x)是增函数,则f(-2),f(1),f(-3)的大小关系是( )
| A、f(1)>f(-3)>f(-2) |
| B、f(1)>f(-2)>f(-3) |
| C、f(1)<f(-3)<f(-2) |
| D、f(1)<f(-2)<f(-3) |
如图所示的程序框图中,输入x=2,则输出的结果是( )


| A、1 | B、2 | C、3 | D、4 |