题目内容
3.已知向量$\overrightarrow{{e}_{1}}$与$\overrightarrow{{e}_{2}}$不共线,且向量$\overrightarrow{AB}$=$\overrightarrow{{e}_{1}}$+m$\overrightarrow{{e}_{2}}$,$\overrightarrow{AC}$=n$\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$,若A,B,C三点共线,则实数m,n( )| A. | mn=1 | B. | mn=-1 | C. | m+n=1 | D. | m+n=-1 |
分析 由题意可得$\overrightarrow{AB}$∥$\overrightarrow{AC}$,再根据两个向量共线的性质可得$\frac{1}{n}$=$\frac{m}{1}$,由此可得结论.
解答 解:由题意可得$\overrightarrow{AB}$∥$\overrightarrow{AC}$,
∴$\overrightarrow{AB}$=λ•$\overrightarrow{AC}$,故有$\frac{1}{n}$=$\frac{m}{1}$,
∴mn=1,
故选:A.
点评 本题主要考查两个向量共线的性质,两个向量坐标形式的运算,属于中档题.

练习册系列答案
相关题目
18.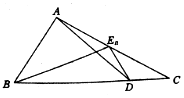 如图,已知点D为△ABC的边BC上一点,$\overrightarrow{BD}$=3$\overrightarrow{DC}$,En(n∈N+)为边AC的一列点,满足$\overrightarrow{{E}_{n}A}$=$\frac{1}{4}$an+1$\overrightarrow{{E}_{n}B}$-(3an+2)$\overrightarrow{{E}_{n}D}$,其中实数列{an}中an>0,a1=1,则{an}的通项公式为( )
如图,已知点D为△ABC的边BC上一点,$\overrightarrow{BD}$=3$\overrightarrow{DC}$,En(n∈N+)为边AC的一列点,满足$\overrightarrow{{E}_{n}A}$=$\frac{1}{4}$an+1$\overrightarrow{{E}_{n}B}$-(3an+2)$\overrightarrow{{E}_{n}D}$,其中实数列{an}中an>0,a1=1,则{an}的通项公式为( )
 如图,已知点D为△ABC的边BC上一点,$\overrightarrow{BD}$=3$\overrightarrow{DC}$,En(n∈N+)为边AC的一列点,满足$\overrightarrow{{E}_{n}A}$=$\frac{1}{4}$an+1$\overrightarrow{{E}_{n}B}$-(3an+2)$\overrightarrow{{E}_{n}D}$,其中实数列{an}中an>0,a1=1,则{an}的通项公式为( )
如图,已知点D为△ABC的边BC上一点,$\overrightarrow{BD}$=3$\overrightarrow{DC}$,En(n∈N+)为边AC的一列点,满足$\overrightarrow{{E}_{n}A}$=$\frac{1}{4}$an+1$\overrightarrow{{E}_{n}B}$-(3an+2)$\overrightarrow{{E}_{n}D}$,其中实数列{an}中an>0,a1=1,则{an}的通项公式为( )| A. | 3•2n-1-2 | B. | 2n-1 | C. | 3n-2 | D. | 2•3n-1-1 |
15.在△ABC中,角A,B,C所对的边分别为a,b,c,根据下列条件解三角形,其中有两个解的是( )
| A. | a=5,b=5,A=50° | B. | a=3,b=4,A=30° | ||
| C. | a=5,b=10,A=30° | D. | a=12,b=10,A=135° |
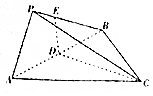 如图所示,三棱锥P-ABC中,△ABC是边长为3的等边三角形,D是线段AB的中点,DE∩PB=E,且DE⊥AB,若∠EDC=120°,PA=$\frac{3}{2}$,PB=$\frac{3\sqrt{3}}{2}$,则三棱锥P-ABC的外接球的表面积为13π.
如图所示,三棱锥P-ABC中,△ABC是边长为3的等边三角形,D是线段AB的中点,DE∩PB=E,且DE⊥AB,若∠EDC=120°,PA=$\frac{3}{2}$,PB=$\frac{3\sqrt{3}}{2}$,则三棱锥P-ABC的外接球的表面积为13π. 已知MOD函数是一个求余函数,记MOD(m,n)表示m除以n的余数,例如MOD(8,3)=2.如图是某个算法的程序框图,若输入m的值为48时,则输出i的值为( )
已知MOD函数是一个求余函数,记MOD(m,n)表示m除以n的余数,例如MOD(8,3)=2.如图是某个算法的程序框图,若输入m的值为48时,则输出i的值为( )