题目内容
12.设函数fa(x)=|x|+|x-a|,当a在实数范围内变化时,在圆盘x2+y2≤1内,且不在任一fa(x)的图象上的点的全体组成的图形的面积为$\frac{3π}{4}$.分析 根据题意,分析可得函数fa(x)=|x|+|x-a|(当a在实数范围内变化)的图象,进而可得在圆盘x2+y2≤1内,且不在任一fa(x)的图象上的点单位圆的$\frac{3}{4}$,由圆的面积公式计算可得答案.
解答  解:根据题意,对于函数fa(x)=|x|+|x-a|,当a变化时,其图象为
解:根据题意,对于函数fa(x)=|x|+|x-a|,当a变化时,其图象为
在圆盘x2+y2≤1内,且不在任一fa(x)的图象上的点单位圆的$\frac{3}{4}$,
则其面积S=$\frac{3}{4}$×π=$\frac{3π}{4}$;
故答案为:$\frac{3π}{4}$.
点评 本题考查函数的图象,关键是分析函数fa(x)=|x|+|x-a|(当a在实数范围内变化)的图象.

练习册系列答案
相关题目
3.已知向量$\overrightarrow{{e}_{1}}$与$\overrightarrow{{e}_{2}}$不共线,且向量$\overrightarrow{AB}$=$\overrightarrow{{e}_{1}}$+m$\overrightarrow{{e}_{2}}$,$\overrightarrow{AC}$=n$\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$,若A,B,C三点共线,则实数m,n( )
| A. | mn=1 | B. | mn=-1 | C. | m+n=1 | D. | m+n=-1 |
20.若集合A={x|x2≤4},B={x|x≥0}.则A∩B=( )
| A. | {x|0≤x≤2} | B. | {x|x≥-2} | C. | {0,1,2} | D. | {1,2} |
17.在平面内的动点(x,y)满足不等式$\left\{\begin{array}{l}{x+y-3≤0}\\{x-y+1≥0}\end{array}\right.$,则z=2x+y的取值范围是( )
| A. | (-∞,+∞) | B. | (-∞,4] | C. | [4,+∞) | D. | [-2,2] |
4.设f(x)为可导函数,且f′(2)=$\frac{1}{2}$,求$\underset{lim}{h→0}$$\frac{f(2-h)-f(2+h)}{h}$的值( )
| A. | 1 | B. | -1 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
1.下列命题中正确的是( )
| A. | 终边在x轴负半轴上的角是零角 | |
| B. | 三角形的内角必是第一、二象限内的角 | |
| C. | 不相等的角的终边一定不相同 | |
| D. | 若β=α+k•360°(k∈Z),则α与β终边相同 |
 已知下列三角形数表假设第行的第二个数为an(n≥2,n∈N*).
已知下列三角形数表假设第行的第二个数为an(n≥2,n∈N*).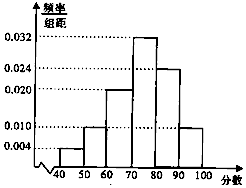 某校从高二年级学生中随机抽取50名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100],得到如图所示的频率分布直方图.
某校从高二年级学生中随机抽取50名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100],得到如图所示的频率分布直方图.