题目内容
14.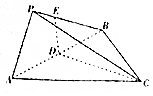 如图所示,三棱锥P-ABC中,△ABC是边长为3的等边三角形,D是线段AB的中点,DE∩PB=E,且DE⊥AB,若∠EDC=120°,PA=$\frac{3}{2}$,PB=$\frac{3\sqrt{3}}{2}$,则三棱锥P-ABC的外接球的表面积为13π.
如图所示,三棱锥P-ABC中,△ABC是边长为3的等边三角形,D是线段AB的中点,DE∩PB=E,且DE⊥AB,若∠EDC=120°,PA=$\frac{3}{2}$,PB=$\frac{3\sqrt{3}}{2}$,则三棱锥P-ABC的外接球的表面积为13π.
分析 由题意得PA2+PB2=AB2,即可得D为△PAB的外心,在CD上取点O1,使O1为等边三角形ABC的中心,在△DEC中,过D作直线与DE垂直,过O1作直线与DC垂直,两条垂线交于点O,则O为球心,在△DEC中求解OC,即可得到球半径,
解答  解:由题意,PA2+PB2=AB2,因为$\left\{\begin{array}{l}{AB⊥DE}\\{AB⊥DC}\\{ED∩DC=D}\end{array}\right.$,∴AD⊥面DEC,
解:由题意,PA2+PB2=AB2,因为$\left\{\begin{array}{l}{AB⊥DE}\\{AB⊥DC}\\{ED∩DC=D}\end{array}\right.$,∴AD⊥面DEC,
∵AD?PAB,AD?ABC,∴面APB⊥面DEC,面ABC⊥面DEC,
在CD上取点O1,使O1为等边三角形ABC的中心,
∵D为△PAB斜边中点,∴在△DEC中,过D作直线与DE垂直,过O1作直线与DC垂直,两条垂线交于点O,则O为球心.
∵∠EDC=90°,∴$∠OD{O}_{1}=3{0}^{0}$,
又∵$D{O}_{1}=\frac{1}{3}CD=\frac{\sqrt{3}}{2}$,∴OO1=$\frac{1}{2}$,三棱锥P-ABC的外接球的半径R=$\sqrt{O{{O}_{1}}^{2}+C{{O}_{1}}^{2}}=\frac{\sqrt{13}}{2}$,
三棱锥P-ABC的外接球的表面积为4πR2=13π,
故答案为:13π.
点评 本题考查了几何体的外接球的表面积,解题关键是要找到球心,求出半径,属于难题.

练习册系列答案
相关题目
4.下列函数中,对于任意的x∈R,满足条件f(x)+f(-x)=0的函数是( )
| A. | $f(x)={x^{\frac{1}{3}}}$ | B. | f(x)=sinx+1 | C. | f(x)=cosx | D. | $f(x)={log_2}({x^2}+1)$ |
9.已知z=$\frac{-3-i}{1+2i}$,则z的虚部为( )
| A. | 1 | B. | -1 | C. | -i | D. | i |
19.已知i为虚数单位,若复数z=$\frac{1-ai}{1+i}$(a∈R)的实部为-3,则|z|=( )
| A. | $\sqrt{10}$ | B. | 2$\sqrt{3}$ | C. | $\sqrt{13}$ | D. | 5 |
3.已知向量$\overrightarrow{{e}_{1}}$与$\overrightarrow{{e}_{2}}$不共线,且向量$\overrightarrow{AB}$=$\overrightarrow{{e}_{1}}$+m$\overrightarrow{{e}_{2}}$,$\overrightarrow{AC}$=n$\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$,若A,B,C三点共线,则实数m,n( )
| A. | mn=1 | B. | mn=-1 | C. | m+n=1 | D. | m+n=-1 |
4.设f(x)为可导函数,且f′(2)=$\frac{1}{2}$,求$\underset{lim}{h→0}$$\frac{f(2-h)-f(2+h)}{h}$的值( )
| A. | 1 | B. | -1 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
 已知下列三角形数表假设第行的第二个数为an(n≥2,n∈N*).
已知下列三角形数表假设第行的第二个数为an(n≥2,n∈N*).