题目内容
8．设A，B是球O的球面上两点，∠AOB=$\frac{π}{3}$，C是球面上的动点，若四面体OABC的体积V的最大值为$\frac{9\sqrt{3}}{4}$，则此时球的表面积为36π．分析 当点C位于垂直于面AOB时，三棱锥O-ABC的体积最大，利用三棱锥O-ABC体积的最大值为$\frac{9\sqrt{3}}{4}$，求出半径，即可求出球O的体积
解答 解：如图所示，当点C位于垂直于面AOB时，三棱锥O-ABC的体积最大，
设球O的半径为R，此时VO-ABC=VC-AOB=$\frac{1}{3}×\frac{1}{2}\\;×{R}^{2}×sin6{0}^{0}×R$×R2×sin60°×R=$\frac{9\sqrt{3}}{4}$，
故R=3，则球O的表面积为4πR2=36π，
故答案为：36π．
点评 本题考查球的半径，考查体积的计算，确定点C位于垂直于面AOB时，三棱锥O-ABC的体积最大是关键．属于中档题
练习册系列答案
相关题目
19．已知i为虚数单位，若复数z=$\frac{1-ai}{1+i}$（a∈R）的实部为-3，则|z|=（ ）
| A． | $\sqrt{10}$ | B． | 2$\sqrt{3}$ | C． | $\sqrt{13}$ | D． | 5 |
16．设曲线y=xn+1（n∈N*）在点（1，1）处的切线与x轴的交点的横坐标为xn，则log2017x1+log2017x2+…+log2017x2016的值为（ ）
| A． | -log20172016 | B． | -1 | C． | log20172016-1 | D． | 1 |
3．已知向量$\overrightarrow{{e}_{1}}$与$\overrightarrow{{e}_{2}}$不共线，且向量$\overrightarrow{AB}$=$\overrightarrow{{e}_{1}}$+m$\overrightarrow{{e}_{2}}$，$\overrightarrow{AC}$=n$\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$，若A，B，C三点共线，则实数m，n（ ）
| A． | mn=1 | B． | mn=-1 | C． | m+n=1 | D． | m+n=-1 |
13．已知复数z满足（1+i）z=2i，则|z|=（ ）
| A． | $\sqrt{2}$ | B． | $\sqrt{3}$ | C． | 2 | D． | 3 |
20．若集合A={x|x2≤4}，B={x|x≥0}．则A∩B=（ ）
| A． | {x|0≤x≤2} | B． | {x|x≥-2} | C． | {0，1，2} | D． | {1，2} |
17．在平面内的动点（x，y）满足不等式$\left\{\begin{array}{l}{x+y-3≤0}\\{x-y+1≥0}\end{array}\right.$，则z=2x+y的取值范围是（ ）
| A． | （-∞，+∞） | B． | （-∞，4] | C． | [4，+∞） | D． | [-2，2] |
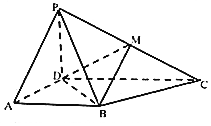如图，四棱锥P-ABCD中，平面PAD⊥平面ABCD，△PAD是正三角形，底面ABCD是直角梯形，AB∥CD，CD⊥AD，CD=2AB=2AD=2，M为PC的中点．