题目内容
计算下列各式的值:
(1)(0.064)-
-(-
)0+[(-2)3]-
+16-0.75;
(2)
lg25+lg2-lg
-log29×log32.
(1)(0.064)-
| 1 |
| 3 |
| 5 |
| 9 |
| 4 |
| 3 |
(2)
| 1 |
| 2 |
| 0.1 |
考点:对数的运算性质,有理数指数幂的化简求值
专题:函数的性质及应用
分析:(1)利用指数的性质和运算法则求解.
(2)利用对数的性质和运算法则求解.
(2)利用对数的性质和运算法则求解.
解答:
解:(1)(0.064)-
-(-
)0+[(-2)3]-
+16-0.75
=0.4-1-1+(-2)-4+2-3
=
-1+
+
=
;…(4分)
(2)
lg25+lg2-lg
-log29×log32
=lg5+lg2-lg10-
-2log23×log32
=1+
-2=-
.…(8分)
| 1 |
| 3 |
| 5 |
| 9 |
| 4 |
| 3 |
=0.4-1-1+(-2)-4+2-3
=
| 10 |
| 4 |
| 1 |
| 16 |
| 1 |
| 8 |
| 27 |
| 16 |
(2)
| 1 |
| 2 |
| 0.1 |
=lg5+lg2-lg10-
| 1 |
| 2 |
=1+
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查指数和对数的化简求值,是基础题,解题时要认真审题,注意运算法则的合理运用.

练习册系列答案
相关题目
在△ABC中,角A,B,C所对边分别为a,b,c,若acosC=b,则△ABC的形状是( )
| A、钝角三角形 |
| B、锐角三角形 |
| C、直角三角形 |
| D、等腰三角形 |
已知A={x|0≤x≤3},B={y|0≤y≤3},下列从集合A到集合B的对应关系不是映射的是( )
A、f:x→y=
| ||
B、f:x→y=
| ||
C、f:x→y=
| ||
D、f:x→y=
|
若函数f(x)=(m2-m-1)xm是幂函数,则f(x)一定( )
| A、是偶函数 |
| B、是奇函数 |
| C、在x∈(-∞,0)上单调递减 |
| D、在x∈(0,+∞)上单调递减 |
在△ABC中,角A,B,C的对边分别是a,b,c,若(a2+c2-b2)tanB=
ac,则角B的值为( )
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知m,n为异面直线,m?平面α,n?平面β,α∩β=l,则直线l( )
| A、与m,n都相交 |
| B、与m,n都不相交 |
| C、与m,n中至少一条相交 |
| D、至多与m,n中的一条相交 |
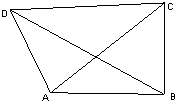 如图:在平面四边形ABCD中,AB=3
如图:在平面四边形ABCD中,AB=3