题目内容
 函数f(x)=Asin(ωx+φ)的图象如图所示,其中A>0,ω>0,0<φ<π.求:
函数f(x)=Asin(ωx+φ)的图象如图所示,其中A>0,ω>0,0<φ<π.求:(1)f(x)的解析式;
(2)f(x)的最大值及f(x)取最大值时x的集合;
(3)求f(x)的单调递增区间.
考点:由y=Asin(ωx+φ)的部分图象确定其解析式,正弦函数的图象
专题:三角函数的图像与性质
分析:(1)根据三角函数的图象即可确定f(x)的解析式;
(2)根据三角函数的性质即可求f(x)的最大值及f(x)取最大值时x的集合;
(3)根据三角函数的单调性即可求f(x)的单调递增区间.
(2)根据三角函数的性质即可求f(x)的最大值及f(x)取最大值时x的集合;
(3)根据三角函数的单调性即可求f(x)的单调递增区间.
解答:
解:(1)函数周期T=2×[3-(-1)]=8=
,
则ω=
,
由图象可知A=3,
则f(x)=3sin(
x+φ),
当x=3时,3×
+φ=π,
解得φ=
,
则f(x)的解析式为f(x)=3sin(
x+
);
(2)当sin(
x+
)=1,即
x+
=
+2kπ;
即x=1+8k时,函数f(x)的取得最大值3,f(x)取最大值时x的集合为{x|1+8k,k∈Z};
(3)由2kπ-
≤
x+
≤2kπ+
,k∈Z,解得8k-3≤x≤8k+1,k∈Z
即f(x)的单调递增区间为[8k-3,8k+1],k∈Z.
| 2π |
| ω |
则ω=
| π |
| 4 |
由图象可知A=3,
则f(x)=3sin(
| π |
| 4 |
当x=3时,3×
| π |
| 4 |
解得φ=
| π |
| 4 |
则f(x)的解析式为f(x)=3sin(
| π |
| 4 |
| π |
| 4 |
(2)当sin(
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| π |
| 2 |
即x=1+8k时,函数f(x)的取得最大值3,f(x)取最大值时x的集合为{x|1+8k,k∈Z};
(3)由2kπ-
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
| π |
| 2 |
即f(x)的单调递增区间为[8k-3,8k+1],k∈Z.
点评:本题主要考查三角函数的解析式的求解以及三角函数性质是综合应用,根据条件确定函数的解析式是解决本题的关键.

练习册系列答案
相关题目
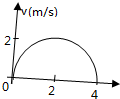 如图所示,一个物体在4s内的速度图象恰好时一个半圆,以下关于物体的运动的说法正确的是( )
如图所示,一个物体在4s内的速度图象恰好时一个半圆,以下关于物体的运动的说法正确的是( )| A、物体前2s作匀加速直线运动,后2s作匀减速直线运动 |
| B、物体在前2s作加速度越来越小的加速运动,后2s作加速度越来越大的减速运动 |
| C、物体在4s内的位移大小是2π(m) |
| D、物体在4s内的位移大小无法确定 |
从空间一点P向二面角α-l-β的两个半平面α,β分别作垂线PE,PF,垂足分别为E,F,若二面角α-l-β的大小为60°,则<
,
>的大小为( )
| PF |
| PE |
| A、30°或150° |
| B、120° |
| C、60°或120° |
| D、60° |
已知函数f(x)=ex-x2,若?x∈[1,2],不等式-m≤f(x)≤m2-4恒成立,则实数m的取值范围是( )
| A、(-∞,1-e] |
| B、[1-e,e] |
| C、[-e,e+1] |
| D、[e,+∞) |