题目内容
在三角形ABC中,角A,B,C的对边分别是a,b,c,且满足acosB=
bsinA,则
sinC-2cosA的最大值为( )
| 2 |
| 3 |
| A、1 | ||
B、
| ||
C、
| ||
| D、2 |
考点:正弦定理
专题:计算题,三角函数的求值,解三角形
分析:运用正弦定理,结合同角公式,求出cosB,sinB,再由诱导公式和两角和的正弦公式,化简所求式子,再由两角差的正弦公式,结合正弦函数的值域,即可得到最大值.
解答:
解:由正弦定理,可得足acosB=
bsinA,
即为sinAcosB=
sinBsinA,
即cosB=
sinB,
由于cos2B+sin2B=1,
解得,sinB=
,cosB=
,
则
sinC-2cosA=
sin(A+B)-2cosA=
(sinAcosB+cosAsinB)-2cosA
=
(
sinA+
cosA)-2cosA=
sinA-cosA
=
(
sinA-
cosA)=
sin(A-α),(其中cosα=
,sinα=
)
则当sin(A-α)=1,即有A=
+α,取得最大值为
.
故选:C.
| 2 |
即为sinAcosB=
| 2 |
即cosB=
| 2 |
由于cos2B+sin2B=1,
解得,sinB=
| ||
| 3 |
| ||
| 3 |
则
| 3 |
| 3 |
| 3 |
=
| 3 |
| ||
| 3 |
| ||
| 3 |
| 2 |
=
| 3 |
| ||
| 3 |
| ||
| 3 |
| 3 |
| ||
| 3 |
| ||
| 3 |
则当sin(A-α)=1,即有A=
| π |
| 2 |
| 3 |
故选:C.
点评:本题考查正弦定理的运用,考查三角函数的化简和求最值,考查两角和差的正弦公式,考查正弦函数的值域,考察了转化思想,属于中档题.

练习册系列答案
 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目
函数y=ln(
-1)的定义域为( )
| 1 |
| x |
| A、(0,1) |
| B、(1,+∞) |
| C、(-∞,0)∪(1,+∞) |
| D、(-∞,1) |
若抛物线y=ax2的焦点坐标是(0,1),则a=( )
| A、1 | ||
B、
| ||
| C、2 | ||
D、
|
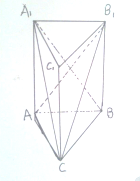 如图,正三棱柱ABC-A1B1C1的边长及棱的长度均为2,求:
如图,正三棱柱ABC-A1B1C1的边长及棱的长度均为2,求: 函数f(x)=Asin(ωx+φ)的图象如图所示,其中A>0,ω>0,0<φ<π.求:
函数f(x)=Asin(ωx+φ)的图象如图所示,其中A>0,ω>0,0<φ<π.求: