题目内容
已知等差数列{an}满足a1=1,前5项和S5=15
(1)求数列{an}的通项公式
(2)求数列{
}的前n项和Tn.
(1)求数列{an}的通项公式
(2)求数列{
| an |
| 2n |
考点:数列的求和
专题:等差数列与等比数列
分析:(1)直接由已知列式求出等差数列的公差,代入等差数列的通项公式得答案;
(2)把(1)中求出的{an}的通项公式代入
,然后由错位相减法求和.
(2)把(1)中求出的{an}的通项公式代入
| an |
| 2n |
解答:
解(1){an}为等差数列,设其公差为d,
由S5=15,得S5=5a1+
d=15,
又a1=1,则5+10d=15,解得d=1,
∴an=a1+(n-1)d=n;
(2)Tn=
+
+…+
①,
Tn=
+
+…+
②,
两式相减得
Tn=
+
+…+
-
=
-
=1-
-
.
∴Tn=2-(
)n-1-
.
由S5=15,得S5=5a1+
| 5×4 |
| 2 |
又a1=1,则5+10d=15,解得d=1,
∴an=a1+(n-1)d=n;
(2)Tn=
| 1 |
| 2 |
| 2 |
| 22 |
| n |
| 2n |
| 1 |
| 2 |
| 1 |
| 22 |
| 2 |
| 23 |
| n |
| 2n+1 |
两式相减得
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 2n |
| n |
| 2n+1 |
=
| ||||
1-
|
| n |
| 2n+1 |
| 1 |
| 2n |
| n |
| 2n+1 |
∴Tn=2-(
| 1 |
| 2 |
| n |
| 2n |
点评:本题考查了等差数列通项公式,考查了等差数列的前n项和,训练了错位相减法求数列的和,是中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知函数f(3x+1)=x2+3x+2,则f(4)=( )
| A、30 | B、6 | C、210 | D、9 |
对函数f(x),若对任意a,b,c∈R,f(a),f(b),f(c)为某一三角形的三边长,则称f(x)为“槑槑函数”,已知f(x)=
是“槑槑函数”,则实数a的取值范围为( )
| ex+a |
| ex+1 |
| A、[0,+∞) | ||
B、[
| ||
| C、[1,2] | ||
| D、[0,1] |
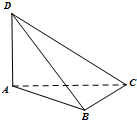 如图,在四面体ABCD中,已知DA⊥面ABC,BC⊥面ABD,BC=BD=2,四面体的三个面DAB、DBC、DCA面积的平方和是8,则∠ADB=
如图,在四面体ABCD中,已知DA⊥面ABC,BC⊥面ABD,BC=BD=2,四面体的三个面DAB、DBC、DCA面积的平方和是8,则∠ADB=