题目内容
对函数f(x),若对任意a,b,c∈R,f(a),f(b),f(c)为某一三角形的三边长,则称f(x)为“槑槑函数”,已知f(x)=
是“槑槑函数”,则实数a的取值范围为( )
| ex+a |
| ex+1 |
| A、[0,+∞) | ||
B、[
| ||
| C、[1,2] | ||
| D、[0,1] |
考点:余弦定理
专题:解三角形
分析:f(x)解析式变形后,由题意得到f(x)>0恒成立,求出a的范围,分0<a≤1与a>1两种情况,利用函数的增减性,以及三角形的三角关系求出a的范围即可.
解答:
解:f(x)=
=1+
,
由题意,f(x)>0恒成立,即
>-1,即a>-ex,
解得:a>0,
①若0<a≤1,则f(x)为增函数,当x取正无穷时,f(x)取最大值1,当x取负无穷时,f(x)取最小值a,
即f(x)值域为(a,1),
又知三角形两边之和大于第三边,故应有a+a≥1,解得:
≤a≤1;
②若a>1,则f(x)为减函数,当x取正无穷时,f(x)取最小值1,当x取负无穷时,f(x)取最大值a,
即f(x)值域为(1,a),同理,有1+1≥a,得1<a≤2,
综上,a的取值范围为[
,2],
故选:B.
| ex+a |
| ex+1 |
| a-1 |
| ex+1 |
由题意,f(x)>0恒成立,即
| a-1 |
| ex+1 |
解得:a>0,
①若0<a≤1,则f(x)为增函数,当x取正无穷时,f(x)取最大值1,当x取负无穷时,f(x)取最小值a,
即f(x)值域为(a,1),
又知三角形两边之和大于第三边,故应有a+a≥1,解得:
| 1 |
| 2 |
②若a>1,则f(x)为减函数,当x取正无穷时,f(x)取最小值1,当x取负无穷时,f(x)取最大值a,
即f(x)值域为(1,a),同理,有1+1≥a,得1<a≤2,
综上,a的取值范围为[
| 1 |
| 2 |
故选:B.
点评:此题考查了余弦定理,函数的增减性,以及三角形三边关系,熟练掌握函数的增减性是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列命题中为真命题的是( )
| A、?x∈R,x2+2x+1=0 | ||
B、?x0∈R,-
| ||
| C、?x∈N*,log2x>0 | ||
| D、?x0∈R,cos x0>x02+2x0+3 |
下列结论正确的是( )
| A、命题“若x2-3x-4=0,则x=4”的逆否命题为“若x≠4,则x2-3x-4=0” |
| B、“x=4”是“x2-3x-4=0”的充分不必要条件 |
| C、已知命题p“若m>0,则方程x2+x-m=0有实根”,则命题p的否定¬p为真命题 |
| D、命题“若m2+n2=0,则m=0且n=0”的否命题是“若m2+n2=0,则m≠0或n≠0” |
函数f(x)=
的定义域为M,g(x)=
的定义域为N,则M∩N=( )
| 1 | ||
|
| x+2 |
| A、[-2,+∞) |
| B、[-2,2) |
| C、(-2,2) |
| D、(-∞,2) |
设S是至少含有两个元素的集合,在S上定义了一个运算“※”(即对任意的a、b∈S,对于有序元素对(a,b),在S中有唯一确定的元素a※b与之对应),若对任意的a、b∈S,有a※(b※a)=b,下列等式中不恒成立的是( )
| A、(a※b)※a=a |
| B、[a※(b※a)]※(a※b)=a |
| C、b※(b※b)=b |
| D、(a※b)※[b※(a※b)]=b |
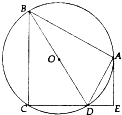 如图,四边形ABCD内接于⊙O,BD是⊙O的直径,AE⊥CD于点E,DA平分∠BDE.
如图,四边形ABCD内接于⊙O,BD是⊙O的直径,AE⊥CD于点E,DA平分∠BDE.