题目内容
已知球的半径为5，球面被互相垂直的两个平面所截，得到的两个圆的公共弦长为2
，若其中一个圆的半径为2
，则另一个圆的半径为（ ）
| 3 |
| 3 |
| A、3 | ||
| B、4 | ||
C、
| ||
D、
|
考点：球内接多面体
专题：计算题,空间位置关系与距离
分析：可以从三个圆心上找关系，构建矩形利用对角线相等即可求解出答案．
解答：
解：设两圆的圆心分别为O1、O2，球心为O，公共弦为AB，其中点为E，则OO1EO2为矩形，
于是OO1=O2E=
，
AE=
AB=
∴O2A=
=4
∴圆O2的半径为4
故选B．
解：设两圆的圆心分别为O1、O2，球心为O，公共弦为AB，其中点为E，则OO1EO2为矩形，于是OO1=O2E=
| 13 |
AE=
| 1 |
| 2 |
| 3 |
∴O2A=
| 13+3 |
∴圆O2的半径为4
故选B．
点评：本题主要考查球的有关概念以及两平面垂直的性质，是对基础知识的考查．解决本题的关键在于得到OO1EO2为矩形．
练习册系列答案
相关题目
如图，甲烷CH4 的分子结构是：碳原子位于正四面体的中心，4个氢原子分别位于正四面体的四个顶点上．设碳原子与4个氢原子连成的四条线段两两组成的角为θ，则cosθ=（ ）| A、0 | ||
B、-
| ||
C、-
| ||
D、-
|
设{an}是由正数组成的等差数列，{bn}是由正数组成的等比数列，且a1=b1，a2003=b2003，则必有（ ）
| A、a1002＞b1002 |
| B、a1002=b1002 |
| C、a1002≥b1002 |
| D、a1002≤b1002 |
下列命题中为真命题的是（ ）
| A、?x∈R，x2+2x+1=0 | ||
B、?x0∈R，-
| ||
| C、?x∈N*，log2x＞0 | ||
| D、?x0∈R，cos x0＞x02+2x0+3 |
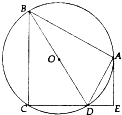如图，四边形ABCD内接于⊙O，BD是⊙O的直径，AE⊥CD于点E，DA平分∠BDE．