题目内容
已知圆C:x2+y2+4x-2y+3=0,点A的坐标是(-1,1),从圆C外一动点P(x,y)向该圆引一条切线,切点为 M,若|PM|=|PA|,则|PM|的最小值是 .
考点:圆的一般方程
专题:直线与圆
分析:求出圆心和半径,根据条件|PM|=|PA|,求出P的轨迹,即可得到结论.
解答:
解:圆的标准方程为(x+2)2+(y-1)2=2,
圆心C坐标为(-2,1),半径R=
,
AC=1<
,则A在圆C内,
∵切线PM与半径CM垂直,
∴|PM|2=|PC|2-|CM|2=|PA|2,
∴(x+2)2+(y-1)2-2=(x+1)2+(y-1)2.
∴x=-
.
∴动点P的轨迹是直线x=-
.
∴|PM|的最小值就是|PA|的最小值.
而|PA|的最小值为A到直线x=-
的距离d=|-
+1|=
,
故答案为:
圆心C坐标为(-2,1),半径R=
| 2 |
AC=1<
| 2 |
∵切线PM与半径CM垂直,
∴|PM|2=|PC|2-|CM|2=|PA|2,
∴(x+2)2+(y-1)2-2=(x+1)2+(y-1)2.
∴x=-
| 1 |
| 2 |
∴动点P的轨迹是直线x=-
| 1 |
| 2 |
∴|PM|的最小值就是|PA|的最小值.
而|PA|的最小值为A到直线x=-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:本题主要考查直线和圆的位置关系的应用,根据条件求出P的轨迹方程是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
如图放置的六条棱长都相等的三棱锥,则这个几何体的侧视图是( )
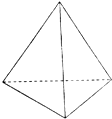

| A、等腰三角形 |
| B、等边三角形 |
| C、直角三角形 |
| D、无两边相等的三角形 |
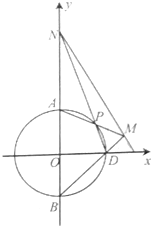 如图所示,已知圆C:x2+y2=r2(r>0)上点
如图所示,已知圆C:x2+y2=r2(r>0)上点