题目内容
已知△ABC中，|
|=|
|=1，∠ACB=120°，O为△ABC的外心，
=λ
+μ
，则λ+μ= ．
| AC |
| CB |
| AO |
| AC |
| AB |
考点：平面向量的基本定理及其意义
专题：平面向量及应用
分析：如图所示，|
|=|
|=1，∠ACB=120°，O为△ABC的外心，可得四边形OACB为菱形，再利用向量的平行四边形法则及其向量基本定理即可得出．
| AC |
| CB |
解答：
解：如图所示，
∵|
|=|
|=1，∠ACB=120°，O为△ABC的外心，
∴四边形OACB为菱形，
∴
=
+
，
又
=λ
+μ
，
则λ+μ=0．
故答案为：0．
∵|
| AC |
| CB |
∴四边形OACB为菱形，
∴
| AB |
| AC |
| AO |
又
| AO |
| AC |
| AB |
则λ+μ=0．
故答案为：0．
点评：本题考查了向量的平行四边形法则、向量基本定理、菱形的性质，考查了推理能力与计算能力，属于中档题．
练习册系列答案
开心练习课课练与单元检测系列答案
开心试卷期末冲刺100分系列答案
相关题目
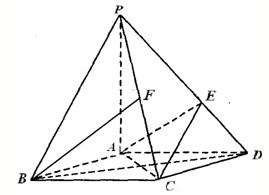如图，在底面是菱形的四棱锥P-ABCD中，∠ABC=60°，PA=AC=a，PB=PD=