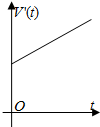题目内容
已知抛物线C:y2=2px(p>0)的焦点F到双曲线x2-
=1的渐近线的距离为
,过焦点F斜率为k的直线与抛物线C交于A、B两点,且
=2
,则|k|=( )
| y2 |
| 3 |
| 3 |
| AF |
| FB |
A、2
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:双曲线的简单性质,抛物线的应用
专题:圆锥曲线的定义、性质与方程
分析:先根据抛物线C的焦点F到双曲线的渐近线距离求出p的值,
再利用直线方程与抛物线C的方程联立,消去x,求出y的值,
利用
=2
,得出yA与yB的关系式,从而求出k的值.
再利用直线方程与抛物线C的方程联立,消去x,求出y的值,
利用
| AF |
| FB |
解答:
解:根据题意,得;
抛物线C:y2=2px(p>0)的焦点为F(
,0),
且F到双曲线x2-
=1的渐近线y=±
x的距离为
,
∴
=
,
解得p=4;
∴过焦点F斜率为k的直线为y=k(x-2),
与抛物线C:y2=8x联立,得:
,
消去x,得y2=8(
+2),
整理,得ky2-8y-16k=0,
解得y=
;
又∵
=2
,
∴(4-xA,-yA)=2(xB-4,yB),
∴yA=-2yB;
当k>0时,yA>0,yB<0,
∴
=2•(-
),
解得k=2
;
当k<0时,yA<0,yB>0,
∴-
=2•
,
解得k=-2
;
∴|k|=2
.
故选:A.
抛物线C:y2=2px(p>0)的焦点为F(
| p |
| 2 |
且F到双曲线x2-
| y2 |
| 3 |
| 3 |
| 3 |
∴
| ||||
|
| 3 |
解得p=4;
∴过焦点F斜率为k的直线为y=k(x-2),
与抛物线C:y2=8x联立,得:
|
消去x,得y2=8(
| y |
| k |
整理,得ky2-8y-16k=0,
解得y=
4±4
| ||
| k |
又∵
| AF |
| FB |
∴(4-xA,-yA)=2(xB-4,yB),
∴yA=-2yB;
当k>0时,yA>0,yB<0,
∴
4+4
| ||
| k |
4-4
| ||
| k |
解得k=2
| 2 |
当k<0时,yA<0,yB>0,
∴-
4+4
| ||
| k |
4-4
| ||
| k |
解得k=-2
| 2 |
∴|k|=2
| 2 |
故选:A.
点评:本题考查了双曲线与抛物线的综合应用问题,也考查了直线与圆锥曲线的综合应用问题,是较难的题目.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
直线m⊥平面α,垂足是O,正四面体ABCD的棱长为4,点C在平面α上运动,点B在直线m上运动,则点O到直线AD的距离的取值范围是( )
A、[
| ||||||||
B、[2
| ||||||||
C、[
| ||||||||
D、[3
|
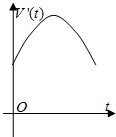
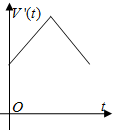
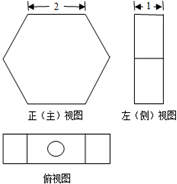 一容器的三视图(正视图是一正六边形)如图,现加入溶液,记溶液液面与容器底面的距离为t,溶液体积为V(t),则函数V(t)的导函数V′(t)的大致图形是( )
一容器的三视图(正视图是一正六边形)如图,现加入溶液,记溶液液面与容器底面的距离为t,溶液体积为V(t),则函数V(t)的导函数V′(t)的大致图形是( )