题目内容
已知方程2m2x2+2mx+1-m2=0(m>1),求证:这个方程有一个正根和一个负根,且正根在(0,1)之间,负根在(-1,0)之间.
考点:函数零点的判定定理
专题:函数的性质及应用
分析:第一步:令函数f(x)=2m2x2+2mx+1-m2(m>1);
第二步:计算f(-1)、f(0)、f(1);
第三步:根据零点存在性定理及二次函数的图象,判断零点所在区间,即可得原方程实根所在区间.
第二步:计算f(-1)、f(0)、f(1);
第三步:根据零点存在性定理及二次函数的图象,判断零点所在区间,即可得原方程实根所在区间.
解答:
证明:令函数f(x)=2m2x2+2mx+1-m2,
∵m>1,∴f(x)为一元二次函数,且
f(-1)=2m2-2m+1-m2=(m-1)2>0,
f(0)=1-m2<0,
f(1)=2m2+2m+1-m2=(m+1)2>0,
f(-1)•f(0)<0,f(0)•f(1)<0,
由零点存在性定理及二次函数的图象知,
方程2m2x2+2mx+1-m2=0(m>1)有一个正根和一个负根,
且正根在(0,1)之间,负根在(-1,0)之间.
∵m>1,∴f(x)为一元二次函数,且
f(-1)=2m2-2m+1-m2=(m-1)2>0,
f(0)=1-m2<0,
f(1)=2m2+2m+1-m2=(m+1)2>0,
f(-1)•f(0)<0,f(0)•f(1)<0,
由零点存在性定理及二次函数的图象知,
方程2m2x2+2mx+1-m2=0(m>1)有一个正根和一个负根,
且正根在(0,1)之间,负根在(-1,0)之间.
点评:本题较基础,主要考查了零点存在性定理,关键是理解方程的实根、函数的零点及函数图象与x轴交点的关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
如果(x2+x+1)(x+m)5展开式中所有项的系数是96,则展开式中x3项的系数是( )
| A、15 | B、20 | C、25 | D、45 |
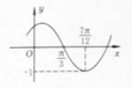 函数f(x)=Asin(ωx+φ)(其中A>0,|φ|<
函数f(x)=Asin(ωx+φ)(其中A>0,|φ|<| π |
| 2 |
A、向右平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向左平移
|
 如图,设O是?ABCD所在平面外的任一点,已知
如图,设O是?ABCD所在平面外的任一点,已知