题目内容
定义在R上的函数f（x）满足f（x+2）-f（x-2）=0，当2≤x≤6时，f（x）=[（
）|x-m|]+n，且f（8）=31，m，n均为正整数，求m，n的值．
| 1 |
| 2 |
考点：函数的周期性
专题：函数的性质及应用
分析：由f（x+2）-f（x-2）=0得到函数为周期是4的周期函数，然后利用f（8）=31解讨论指数方程即可得到结论．
解答：
解：∵f（x+2）-f（x-2）=0，
∴f（x+2）=f（x-2），即f（x+4）=f（x），
即函数的周期是4．
∴f（8）=f（4）=31，
∵当2≤x≤6时，f（x）=[（
）|x-m|]+n，
∴f（4）=[（
）|4-m|]+n=31，
∵m，n均为正整数，
∴当m=4时，即n=30时，方程才成立．
故m=4，n=30．
∴f（x+2）=f（x-2），即f（x+4）=f（x），
即函数的周期是4．
∴f（8）=f（4）=31，
∵当2≤x≤6时，f（x）=[（
| 1 |
| 2 |
∴f（4）=[（
| 1 |
| 2 |
∵m，n均为正整数，
∴当m=4时，即n=30时，方程才成立．
故m=4，n=30．
点评：本题主要考查函数周期性的应用，以及指数方程的解法，考查学生的计算能力．
练习册系列答案
相关题目
三条直线x=2，x-y-1=0，x+ky=0相交于一点，则k的值为（ ）
| A、-2 | ||
B、-
| ||
| C、2 | ||
D、
|
已知数列{an}，{bn}（n∈N*）都是公差为1的等差数列，其首项分别为a1，b1，且a1+b1=5，则数列{an+bn}的前10项的和等于（ ）
| A、85 | B、95 |
| C、120 | D、140 |
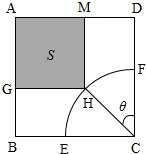如图，体育馆计划用运动场的边角地建造一个矩形健身室，四边形ABCD是一块正方形地皮，边长为a（a＞40m），扇形CEF是运动场的一部分，半径为40m，矩形AGHM就是计划的健身室，其中G、M分别在AB、AD上，H在