Question

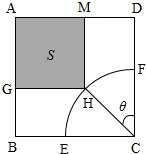如图，体育馆计划用运动场的边角地建造一个矩形健身室，四边形ABCD是一块正方形地皮，边长为a（a＞40m），扇形CEF是运动场的一部分，半径为40m，矩形AGHM就是计划的健身室，其中G、M分别在AB、AD上，H在

EF

上．设矩形AGHM的面积为S，∠HCF=θ，试将S表达为θ的函数，并且指出当H在

EF

上何处时，健身室的面积最大，最大值是多少？

Answer 1

考点：扇形面积公式

专题：计算题,三角函数的求值,解三角形

分析：先利用线段之间的关系求出矩形AGHM的面积S关于θ的函数关系式，再借助于θ的取值范围以及二次函数在闭区间上求最值的方法即可求出矩形面积最大值，以及H在

EF

上的位置．

解答： 解：延长MH交BC于点R，则AM=AD-MD=a-40sinθ，AG=AB-BG=a-40cosθ，
于是，S=AG•AM=a²-40a（sinθ+cosθ）+1600sinθ•cosθ
令t=sinθ+cosθ=

2

sin（θ+45°），则sinθcosθ=

t2-1

2

，
所以S=a²-40at+1600

t2-1

2

=800（t-

a

40

）²+

a2

2

-800．
∵0⁰≤θ≤90⁰
∴1≤t≤

2

∴当t=1，即θ=0°或90°时，S有最大值a²-40a，
此时点H在E或F点，矩形面积最大值为a²-40a．

点评：本题主要考查三角函数知识的应用问题．解决本题的关键在于求出矩形CRGP的面积S关于θ的函数关系式．