题目内容
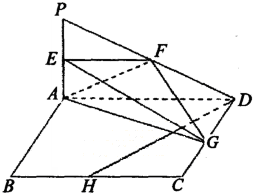 如图,四边形ABCD为正方形,PA⊥平面ABCD,且AD=2PA,E、F、G、H分别是线段PA、PD、CD、BC的中点.
如图,四边形ABCD为正方形,PA⊥平面ABCD,且AD=2PA,E、F、G、H分别是线段PA、PD、CD、BC的中点.(Ⅰ)求证:BC∥平面EFG;
(Ⅱ)求证:DH⊥平面AEG.
考点:直线与平面垂直的判定,直线与平面平行的判定
专题:空间位置关系与距离
分析:(Ⅰ)由三角形中位线定理得AD∥EF,由平行公理得BC∥EF,由此能证明BC∥平面EFG.
(Ⅱ)由线面垂直得PA⊥DH,即AE⊥DH,由三角形全等得DH⊥AG,由此能证明DH⊥平面AEG.
(Ⅱ)由线面垂直得PA⊥DH,即AE⊥DH,由三角形全等得DH⊥AG,由此能证明DH⊥平面AEG.
解答:
解:(Ⅰ)因为E,F分别为PA,PD中点,所以AD∥EF,
因为BC∥AD,所以BC∥EF,…(2分)
因为BC?平面EFG,EF?平面EFG,…(4分)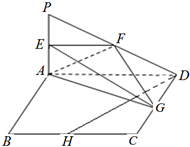
所以BC∥平面EFG.…(6分)
(Ⅱ)因为PA⊥平面ABCD,所以PA⊥DH,
即AE⊥DH,…(8分)
因为△ADG≌△DCH,
所以∠HDC=∠DAG,
∠AGD+∠DAG=90°,
所以∠AGD+∠HDC=90°,
所以DH⊥AG,
又因为AE∩AG=A,所以DH⊥平面AEG.…(12分)
因为BC∥AD,所以BC∥EF,…(2分)
因为BC?平面EFG,EF?平面EFG,…(4分)

所以BC∥平面EFG.…(6分)
(Ⅱ)因为PA⊥平面ABCD,所以PA⊥DH,
即AE⊥DH,…(8分)
因为△ADG≌△DCH,
所以∠HDC=∠DAG,
∠AGD+∠DAG=90°,
所以∠AGD+∠HDC=90°,
所以DH⊥AG,
又因为AE∩AG=A,所以DH⊥平面AEG.…(12分)
点评:本题考查直线与平面平行的证明,考查直线与平面垂直的证明,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
定义在R上的函数f(x)满足f(x+2)=f(x)+1,且x∈[0,1]时,f(x)=4x,x∈(1,2)时,f(x)=
,令g(x)=2f(x)-x-4x∈[-6,2],则函数g(x)的零点个数为( )
| f(1) |
| x |
| A、9 | B、8 | C、7 | D、6 |
已知等差数列{an}的前n项和为Sn,若
=a1
+a20
,且A、B、C三点共线(该直线不过点O),则S20=( )
| OB |
| OA |
| OC |
| A、10 | B、11 | C、20 | D、21 |
如果0<x<1,0<y<1,那么关于0<
<1( )
| x |
| y |
| A、正确 | B、错误 | C、不确定 |
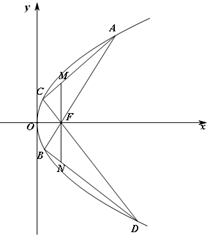 已知抛物线y2=2px(p>0)的焦点F到直线x-y+1=0的距离为
已知抛物线y2=2px(p>0)的焦点F到直线x-y+1=0的距离为