题目内容
2．函数f（x）=$\left\{\begin{array}{l}{{2}^{x}-2，x≤1}\\{-lo{g}_{2}（x+1），x＞1}\end{array}\right.$且f（a）=-3，则f（5-a）=（ ）| A． | -$\frac{7}{4}$ | B． | -$\frac{5}{4}$ | C． | -$\frac{3}{4}$ | D． | -$\frac{1}{4}$ |
分析 利用导函数的解析式，列出方程求解即可．
解答 解：函数f（x）=$\left\{\begin{array}{l}{{2}^{x}-2，x≤1}\\{-lo{g}_{2}（x+1），x＞1}\end{array}\right.$且f（a）=-3，
当a≤1时，2a-2=-3，无解．
当a＞1时，-log2（a+1）=-3，解得a=7．
f（5-a）=f（-2）=2-2-2=$-\frac{7}{4}$．
故选：A．
点评 本题考查分段函数的应用，考查计算能力．
练习册系列答案
相关题目
13．
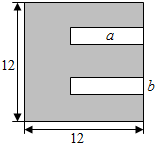如图所示：一张正方形状的黑色硬质板，剪去两个一样的小矩形得到一个“E”形的图形，设小矩形的长、宽分别为a，b（2≤a≤10），剪去部分的面积为8，则$\frac{1}{b+1}$+$\frac{9}{a+9}$的最大值为（ ）
如图所示：一张正方形状的黑色硬质板，剪去两个一样的小矩形得到一个“E”形的图形，设小矩形的长、宽分别为a，b（2≤a≤10），剪去部分的面积为8，则$\frac{1}{b+1}$+$\frac{9}{a+9}$的最大值为（ ）| A． | 1 | B． | $\frac{11}{10}$ | C． | $\frac{6}{5}$ | D． | 2 |
7．用反证法证明“a+b$\sqrt{2}$（a、b∈Z）是无理数”时，假设正确的是（ ）
| A． | 假设$\sqrt{2}$是有理数 | B． | 假设b$\sqrt{2}$（b∈Z）是有理数 | ||
| C． | 假设a+$\sqrt{2}$（a∈Z）是有理数 | D． | 假设a+b$\sqrt{2}$（a、b∈Z）是有理数 |