题目内容
5．已知向量$\overrightarrow{a}$=（4，-2），$\overrightarrow{b}$=（x，1），若$\overrightarrow{a}$∥$\overrightarrow{b}$，则|$\overrightarrow{a}$+$\overrightarrow{b}$|=$\sqrt{5}$．分析 根据两向量平行的坐标表示，列出方程求出x的值，再求$\overrightarrow{a}$+$\overrightarrow{b}$的模长|$\overrightarrow{a}$+$\overrightarrow{b}$|．
解答 解：∵向量$\overrightarrow{a}$=（4，-2），$\overrightarrow{b}$=（x，1），且$\overrightarrow{a}$∥$\overrightarrow{b}$，
∴-2x-4×1=0，解得x=-2；
∴$\overrightarrow{b}$=（-2，1），
∴$\overrightarrow{a}$+$\overrightarrow{b}$=（2，-1），
∴|$\overrightarrow{a}$+$\overrightarrow{b}$|=$\sqrt{{2}^{2}{+（-1）}^{2}}$=$\sqrt{5}$．
故答案为：$\sqrt{5}$．
点评 本题考查了平面向量的坐标运算问题，也考查了向量平行与模长的计算问题，是基础题目．
练习册系列答案
单元全能练考卷系列答案
新黄冈兵法密卷系列答案
相关题目
15．已知l、m、n是三条不同的直线，α、β是两个不重合的平面，给出下列四个命题：
①若l⊥m，m⊥n，则l∥n；
②若m⊥α，n⊥β，α⊥β，则m⊥n；
③若m∥α，n∥β，α∥β，则m∥n；
④若l与α、β所成角相等，且m⊥α，n⊥β，则l与m、n所成角相等．
其中真命题是（ ）
①若l⊥m，m⊥n，则l∥n；
②若m⊥α，n⊥β，α⊥β，则m⊥n；
③若m∥α，n∥β，α∥β，则m∥n；
④若l与α、β所成角相等，且m⊥α，n⊥β，则l与m、n所成角相等．
其中真命题是（ ）
| A． | ①和② | B． | ①和③ | C． | ②和④ | D． | ①和④ |
16．
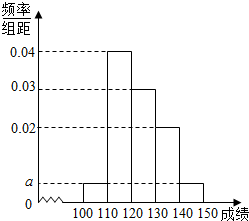贵阳市某中学高三第一次摸底考试中100名学生数学成绩的频率分布直方图如图所示，其中成绩分组区间是[100，110），[110，120），[120，130），[130，140），[140，150]．
（Ⅰ）求图中a的值；
（Ⅱ）根据频率分布直方图，估计这100名学生数学成绩的平均分；
（Ⅲ）若这100名学生数学成绩某些分数段的人数（x）与语文成绩相应分数段的人数（y）之比如下表所示，求语文成绩在[100，140）之外的人数．
贵阳市某中学高三第一次摸底考试中100名学生数学成绩的频率分布直方图如图所示，其中成绩分组区间是[100，110），[110，120），[120，130），[130，140），[140，150]．（Ⅰ）求图中a的值；
（Ⅱ）根据频率分布直方图，估计这100名学生数学成绩的平均分；
（Ⅲ）若这100名学生数学成绩某些分数段的人数（x）与语文成绩相应分数段的人数（y）之比如下表所示，求语文成绩在[100，140）之外的人数．
| 分数段 | [100，110） | [110，120） | [120，130） | [130，140） |
| x：y | 1：1 | 2：1 | 3：4 | 4：5 |
13．
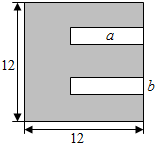如图所示：一张正方形状的黑色硬质板，剪去两个一样的小矩形得到一个“E”形的图形，设小矩形的长、宽分别为a，b（2≤a≤10），剪去部分的面积为8，则$\frac{1}{b+1}$+$\frac{9}{a+9}$的最大值为（ ）
如图所示：一张正方形状的黑色硬质板，剪去两个一样的小矩形得到一个“E”形的图形，设小矩形的长、宽分别为a，b（2≤a≤10），剪去部分的面积为8，则$\frac{1}{b+1}$+$\frac{9}{a+9}$的最大值为（ ）| A． | 1 | B． | $\frac{11}{10}$ | C． | $\frac{6}{5}$ | D． | 2 |
15．已知f（x）是定义在R上的奇函数，当x≥0时，f（x）=3x-1-m（m为常数），则f（log3$\frac{1}{5}$）=（ ）
| A． | 4 | B． | -4 | C． | $\frac{4}{5}$ | D． | -$\frac{4}{5}$ |