题目内容
3.奇函数f(x)在(0,+∞)上递增,且f(-2)=0,则不等式 $\frac{f(x)-f(-x)}{x}$<0的解集为( )| A. | (-∞,-2)∪(0,2) | B. | (-2,0)∪(0,2) | C. | (-∞,-2)∪(2,+∞) | D. | (-2,0)∪(2,+∞) |
分析 根据函数奇偶性和单调性之间的关系,将不等式进行转化即可得到结论.
解答 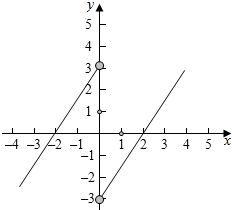 解:∵函数f(x)是奇函数,且在(0,+∞)上是增函数,又f(-2)=0,
解:∵函数f(x)是奇函数,且在(0,+∞)上是增函数,又f(-2)=0,
∴f(x)在(-∞,0)上是增函数,且f(2)=-f(-2)=0,
∴当x>2或-2<x<0时,f(x)>0,当x<-2或0<x<2时,f(x)<0,
作出f(x)的草图,如图所示:
则不等式 $\frac{f(x)-f(-x)}{x}$<0等价为$\frac{2f(x)}{x}$<0:
即$\left\{\begin{array}{l}{x>0}\\{f(x)<0}\end{array}\right.$或$\left\{\begin{array}{l}{x<0}\\{f(x)>0}\end{array}\right.$,
解得0<x<2或-2<x<0,
∴xf(x)<0的解集为:(-2,0)∪(0,2),
故选:B
点评 本题主要考查不等式的解集,利用函数奇偶性和单调性之间的关系是解决本题的关键.

练习册系列答案
相关题目
13.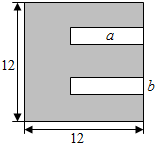 如图所示:一张正方形状的黑色硬质板,剪去两个一样的小矩形得到一个“E”形的图形,设小矩形的长、宽分别为a,b(2≤a≤10),剪去部分的面积为8,则$\frac{1}{b+1}$+$\frac{9}{a+9}$的最大值为( )
如图所示:一张正方形状的黑色硬质板,剪去两个一样的小矩形得到一个“E”形的图形,设小矩形的长、宽分别为a,b(2≤a≤10),剪去部分的面积为8,则$\frac{1}{b+1}$+$\frac{9}{a+9}$的最大值为( )
 如图所示:一张正方形状的黑色硬质板,剪去两个一样的小矩形得到一个“E”形的图形,设小矩形的长、宽分别为a,b(2≤a≤10),剪去部分的面积为8,则$\frac{1}{b+1}$+$\frac{9}{a+9}$的最大值为( )
如图所示:一张正方形状的黑色硬质板,剪去两个一样的小矩形得到一个“E”形的图形,设小矩形的长、宽分别为a,b(2≤a≤10),剪去部分的面积为8,则$\frac{1}{b+1}$+$\frac{9}{a+9}$的最大值为( )| A. | 1 | B. | $\frac{11}{10}$ | C. | $\frac{6}{5}$ | D. | 2 |
15.已知f(x)是定义在R上的奇函数,当x≥0时,f(x)=3x-1-m(m为常数),则f(log3$\frac{1}{5}$)=( )
| A. | 4 | B. | -4 | C. | $\frac{4}{5}$ | D. | -$\frac{4}{5}$ |
12.已知数列{an}的首项a1=2,数列{bn}为等比数列,且${b_n}=\frac{{{a_{n+1}}}}{a_n}$,若b10b11=2,则a21=( )
| A. | 29 | B. | 210 | C. | 211 | D. | 212 |
13.已知直线x=$\frac{π}{4}$和x=$\frac{5π}{4}$是函数f(x)=2sin(ωx+φ)(ω>0,0<φ<π)图象的两条相邻的对称轴,则φ=( )
| A. | $\frac{π}{4}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{2}$ | D. | $\frac{3π}{4}$ |