题目内容
6．函数$f（x）={log_x}（6{x^2}-7x+2）$的定义域是（ ）| A． | $（0{，_{\;}}\frac{1}{2}）∪（\frac{2}{3}{，_{\;}}1）∪（1{，_{\;}}+∞）$ | B． | $（-∞{，_{\;}}\frac{1}{2}）∪（\frac{2}{3}{，_{\;}}+∞）$ | ||
| C． | $（\frac{1}{2}{，_{\;}}\frac{2}{3}）$ | D． | $（0{，_{\;}}\frac{1}{2}）∪（\frac{2}{3}{，_{\;}}1）∪（1{，_{\;}}\frac{3}{2}）$ |
分析 要使函数$f（x）={log_x}（6{x^2}-7x+2）$有意义，则应满足$\left\{\begin{array}{l}{6{x}^{2}-7x+2＞0}\\{x＞0}\\{x≠1}\end{array}\right.$，解不等式组即可得到函数的定义域．
解答 解：要使函数$f（x）={log_x}（6{x^2}-7x+2）$有意义，
则$\left\{\begin{array}{l}{6{x}^{2}-7x+2＞0}\\{x＞0}\\{x≠1}\end{array}\right.$，
解得：$0＜x＜\frac{1}{2}$或$x＞\frac{2}{3}$且x≠1．
故函数$f（x）={log_x}（6{x^2}-7x+2）$的定义域是：（0，$\frac{1}{2}$）∪（$\frac{2}{3}$，1）∪（1，+∞）．
故选：A．
点评 本题考查了函数的定义域及其求法，考查了对数的运算性质和一元二次不等式的解法，是基础题．
练习册系列答案
寒假天地重庆出版社系列答案
相关题目
16．
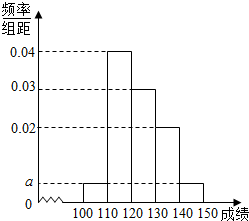贵阳市某中学高三第一次摸底考试中100名学生数学成绩的频率分布直方图如图所示，其中成绩分组区间是[100，110），[110，120），[120，130），[130，140），[140，150]．
（Ⅰ）求图中a的值；
（Ⅱ）根据频率分布直方图，估计这100名学生数学成绩的平均分；
（Ⅲ）若这100名学生数学成绩某些分数段的人数（x）与语文成绩相应分数段的人数（y）之比如下表所示，求语文成绩在[100，140）之外的人数．
贵阳市某中学高三第一次摸底考试中100名学生数学成绩的频率分布直方图如图所示，其中成绩分组区间是[100，110），[110，120），[120，130），[130，140），[140，150]．（Ⅰ）求图中a的值；
（Ⅱ）根据频率分布直方图，估计这100名学生数学成绩的平均分；
（Ⅲ）若这100名学生数学成绩某些分数段的人数（x）与语文成绩相应分数段的人数（y）之比如下表所示，求语文成绩在[100，140）之外的人数．
| 分数段 | [100，110） | [110，120） | [120，130） | [130，140） |
| x：y | 1：1 | 2：1 | 3：4 | 4：5 |
15．已知f（x）是定义在R上的奇函数，当x≥0时，f（x）=3x-1-m（m为常数），则f（log3$\frac{1}{5}$）=（ ）
| A． | 4 | B． | -4 | C． | $\frac{4}{5}$ | D． | -$\frac{4}{5}$ |