题目内容
19.已知空间直角坐标系o-xyz中的点A的坐标为(1,1,1),平面α过点A且与直线OA垂直,动点P(x,y,z)是平面α内的任一点,则点P的坐标满足的条件是x+y+z=3.分析 通过平面α过点A且与直线OA垂直,利用勾股定理即可求点P的坐标满足的条件;
解答 解:因为OA⊥α,所以OA⊥AP,P(x,y,z).
$\overrightarrow{OA}$=(1,1,1),$\overrightarrow{AP}=(x-1,y-1,z-1)$
由勾股定理可得:|OA|2+|AP|2=|OP|2,
即3+(x-1)2+(y-1)2+(z-1)2=x2+y2+z2,
化简得:x+y+z=3.
点P的坐标满足的条件是:x+y+z=3.
故答案为:x+y+z=3.
点评 本题考查空间想象能力,计算能力,转化思想,空间两点距离公式的应用.

练习册系列答案
 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
7.用反证法证明“a+b$\sqrt{2}$(a、b∈Z)是无理数”时,假设正确的是( )
| A. | 假设$\sqrt{2}$是有理数 | B. | 假设b$\sqrt{2}$(b∈Z)是有理数 | ||
| C. | 假设a+$\sqrt{2}$(a∈Z)是有理数 | D. | 假设a+b$\sqrt{2}$(a、b∈Z)是有理数 |
9.已知函数y=f(x)是定义在上的奇函数,且当x>0时,f(x)=2x-1-3,则f(f(1))=( )
| A. | 1 | B. | -1 | C. | 2 | D. | -2 |
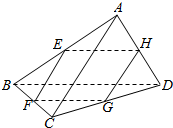 如图所示,在三棱锥A-BCD中,E,F,G,H分别是棱AB,BC,CD,DA的中点,则当AC,BD满足条件AC=BD时,四边形EFGH为菱形.
如图所示,在三棱锥A-BCD中,E,F,G,H分别是棱AB,BC,CD,DA的中点,则当AC,BD满足条件AC=BD时,四边形EFGH为菱形.