题目内容
求函数y=
的值域.
| 1-2cosx |
| 1+2cosx |
考点:函数的值域
专题:三角函数的求值
分析:先将函数y=
转化为cosx=
,然后利用余弦函数的取值范围建立不等式,解之即可求出y的值域.
| 1-2cosx |
| 1+2cosx |
| 1-y |
| 2+2y |
解答:
解:∵y=
,
∴cosx=
,
∵-1≤cosx≤1,
∴|cosx|=|
|≤1,即(1-y)2≤(2+2y)2,解得:y≤-3或y≥-
,
∴函数y=
的值域为(-∞,-3]∪[-
,+∞).
| 1-2cosx |
| 1+2cosx |
∴cosx=
| 1-y |
| 2+2y |
∵-1≤cosx≤1,
∴|cosx|=|
| 1-y |
| 2+2y |
| 1 |
| 3 |
∴函数y=
| 1-2cosx |
| 1+2cosx |
| 1 |
| 3 |
点评:本题考查函数的值域,解决的关键是变换变量的位置,考查学生综合分析与应用的能力以及运算求解的能力,属于中档题.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
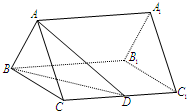 如图,已知正三棱柱ABC-A1B1C1的底面边长是2,D是侧棱CC1的中点,直线AD与侧面BB1C1C所成的角为45°.
如图,已知正三棱柱ABC-A1B1C1的底面边长是2,D是侧棱CC1的中点,直线AD与侧面BB1C1C所成的角为45°.