题目内容
设函数f(x)=ex-ax+a(a∈R),其图象与x轴交于A(x1,0),B(x2,0)两点,且x1<x2.
(1)求a的取值范围;
(2)证明:f′(
)<0(f′(x)为函数f(x)的导函数);
(3)设点C在函数y=f(x)的图象上,且△ABC为等腰直角三角形,记
=t,求(a-1)(t-1)的值.
(1)求a的取值范围;
(2)证明:f′(
| x1x2 |
(3)设点C在函数y=f(x)的图象上,且△ABC为等腰直角三角形,记
|
考点:利用导数研究函数的单调性
专题:导数的综合应用
分析:(1)由f(x)=ex-ax+a,知f′(x)=ex-a,再由a的符号进行分类讨论,能求出f(x)的单调区间,然后根据交点求出a的取值范围;
(2)由x1、x2的关系,求出f′(
)<0,然后再根据f′(x)=ex-a的单调性,利用不等式的性质,问题得以证明;
(3)利用△ABC为等腰直角三角形的性质,求出y0+
=0,然后得到关于参数a的方程at-
(1+t2)+
(t2-1)=0,求得问题的答案.
(2)由x1、x2的关系,求出f′(
| x1+x2 |
| 2 |
(3)利用△ABC为等腰直角三角形的性质,求出y0+
| x2-x1 |
| 2 |
| a |
| 2 |
| 1 |
| 2 |
解答:
解:(1)∵f(x)=ex-ax+a,
∴f'(x)=ex-a,
若a≤0,则f'(x)>0,则函数f(x)是单调增函数,这与题设矛盾.
∴a>0,令f'(x)=0,则x=lna,
当f'(x)<0时,x<lna,f(x)是单调减函数,
当f'(x)>0时,x>lna,f(x)是单调增函数,
于是当x=lna时,f(x)取得极小值,
∵函数f(x)=ex-ax+a(a∈R)的图象与x轴交于两点A(x1,0),B(x2,0)(x1<x2),
∴f(lna)=a(2-lna)<0,即a>e2,
此时,存在1<lna,f(1)=e>0,
存在3lna>lna,f(3lna)=a3-3alna+a>a3-3a2+a>0,
又由f(x)在(-∞,lna)及(lna,+∞)上的单调性及曲线在R上不间断,
可知a>e2为所求取值范围.
(2)∵
,
∴两式相减得a=
.
记
=s(s>0),则f′(
)=e
-
=
[2s-(es-e-s)],
设g(s)=2s-(es-e-s),
则g'(s)=2-(es+e-s)<0,
∴g(s)是单调减函数,
则有g(s)<g(0)=0,而
>0,
∴f′(
)<0.
又f'(x)=ex-a是单调增函数,且
>
∴f′(
)<0.
(3)依题意有exi-axi+a=0,则a(xi-1)=exi>0⇒xi>1(i=1,2).
于是e
=a
,在等腰三角形ABC中,显然C=90°,
∴x0=
∈(x1 ,x2),即y0=f(x0)<0,
由直角三角形斜边的中线性质,可知
=-y0,
∴y0+
=0,
即e
-
(x1+x2)+a+
=0,
∴a
-
(x1+x2)+a+
=0,
即a
-
[(x1-1)+(x2-1)]+
=0.
∵x1-1≠0,则a
-
(1+
)+
=0,
又
=t,
∴at-
(1+t2)+
(t2-1)=0,
即a=1+
,
∴(a-1)(t-1)=2.
∴f'(x)=ex-a,
若a≤0,则f'(x)>0,则函数f(x)是单调增函数,这与题设矛盾.
∴a>0,令f'(x)=0,则x=lna,
当f'(x)<0时,x<lna,f(x)是单调减函数,
当f'(x)>0时,x>lna,f(x)是单调增函数,
于是当x=lna时,f(x)取得极小值,
∵函数f(x)=ex-ax+a(a∈R)的图象与x轴交于两点A(x1,0),B(x2,0)(x1<x2),
∴f(lna)=a(2-lna)<0,即a>e2,
此时,存在1<lna,f(1)=e>0,
存在3lna>lna,f(3lna)=a3-3alna+a>a3-3a2+a>0,
又由f(x)在(-∞,lna)及(lna,+∞)上的单调性及曲线在R上不间断,
可知a>e2为所求取值范围.
(2)∵
|
∴两式相减得a=
| ex2-ex1 |
| x2-x1 |
记
| x2-x1 |
| 2 |
| x1+x2 |
| 2 |
| x1+x2 |
| 2 |
| ex2-ex1 |
| x2-x1 |
e
| ||
| 2s |
设g(s)=2s-(es-e-s),
则g'(s)=2-(es+e-s)<0,
∴g(s)是单调减函数,
则有g(s)<g(0)=0,而
e
| ||
| 2s |
∴f′(
| x1+x2 |
| 2 |
又f'(x)=ex-a是单调增函数,且
| x1+x2 |
| 2 |
| x1x2 |
∴f′(
| x1x2 |
(3)依题意有exi-axi+a=0,则a(xi-1)=exi>0⇒xi>1(i=1,2).
于是e
| x1+x2 |
| 2 |
| (x1-1)(x2-1) |
∴x0=
| x1+x2 |
| 2 |
由直角三角形斜边的中线性质,可知
| x2-x1 |
| 2 |
∴y0+
| x2-x1 |
| 2 |
即e
| x1+x2 |
| 2 |
| a |
| 2 |
| x2-x1 |
| 2 |
∴a
| (x1-1)(x2-1) |
| a |
| 2 |
| x2-x1 |
| 2 |
即a
| (x1-1)(x2-1) |
| a |
| 2 |
| (x2-1)-(x1-1) |
| 2 |
∵x1-1≠0,则a
|
| a |
| 2 |
| x2-1 |
| x1-1 |
| ||
| 2 |
又
|
∴at-
| a |
| 2 |
| 1 |
| 2 |
即a=1+
| 2 |
| t-1 |
∴(a-1)(t-1)=2.
点评:本题属于难题,考察了分类讨论的思想,转化思想,方程思想,做题要认真仔细,方法要明,过程要严谨,能提高分析问题解决问题的能力.

练习册系列答案
相关题目
若函数f(x)=1-2sin2(x+
)(x∈R),则f(x)是( )
| π |
| 4 |
| A、最小正周期为π的偶函数 | ||
| B、最小正周期为π的奇函数 | ||
C、最小正周期为
| ||
D、最小正周期为
|
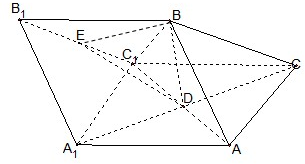 如图,三棱柱ABC-A1B1C1中,AB=AC=AA1=BC1=2,∠AA1C1=60°,平面ABC1⊥平面AA1C1C,AC1与A1C相交于点D.
如图,三棱柱ABC-A1B1C1中,AB=AC=AA1=BC1=2,∠AA1C1=60°,平面ABC1⊥平面AA1C1C,AC1与A1C相交于点D.