题目内容
已知向量
=（1，0），
=（2，1）．
（1）分别求
+
，2
-3
，|
|；
（2）当k为何值时，k
-
与
+3
平行，平行时它们是同向还是反向？
| a |
| b |
（1）分别求
| a |
| b |
| a |
| b |
| b |
（2）当k为何值时，k
| a |
| b |
| a |
| b |
考点：平面向量共线（平行）的坐标表示,平面向量数量积的坐标表示、模、夹角
专题：平面向量及应用
分析：（1）直接由向量的数乘及坐标加减法运算求
+
，2
-3
，由模的计算公式求|
|；
（2）由向量的数乘及坐标加减法运算求k
-
与
+3
的坐标，然后由向量平行的坐标表示列式计算k的值．
| a |
| b |
| a |
| b |
| b |
（2）由向量的数乘及坐标加减法运算求k
| a |
| b |
| a |
| b |
解答：
解：（1）∵
=（1，0），
=（2，1），
∴
+
=（1，0）+（2，1）=（3，1），
2
-3
=2（1，0）+3（2，1）=（8，3），
|
|=
=
；
（2）∵
=（1，0），
=（2，1），
∴k
-
=k（1，0）-（2，1）=（k-2，-1），
+3
=（1，0）+3（2，1）=（7，3）
∵k
-
与
+3
平行，
∴（k-2）×3-（-1）×7=0，即k=-
．
当k=-
时k
-
与
+3
平行，
此时k
-
=（-
，-1）=-
（7，3）=-
（
+3
），
两向量反向．
| a |
| b |
∴
| a |
| b |
2
| a |
| b |
|
| b |
| 22+12 |
| 5 |
（2）∵
| a |
| b |
∴k
| a |
| b |
| a |
| b |
∵k
| a |
| b |
| a |
| b |
∴（k-2）×3-（-1）×7=0，即k=-
| 1 |
| 3 |
当k=-
| 1 |
| 3 |
| a |
| b |
| a |
| b |
此时k
| a |
| b |
| 7 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| a |
| b |
两向量反向．
点评：平行问题是一个重要的知识点，在高考题中常常出现，常与向量的模、向量的坐标表示等联系在一起，要特别注意垂直与平行的区别．若
=（a1，a2），
=（b1，b2），则
⊥
?a1a2+b1b2=0，
∥
?a1b2-a2b1=0．是基础题．
| a |
| b |
| a |
| b |
| a |
| b |
练习册系列答案
课堂全解字词句段篇章系列答案
步步高口算题卡系列答案
相关题目
若函数f（x）=1-2sin2（x+
）（x∈R），则f（x）是（ ）
| π |
| 4 |
| A、最小正周期为π的偶函数 | ||
| B、最小正周期为π的奇函数 | ||
C、最小正周期为
| ||
D、最小正周期为
|
如图，在四棱锥P-ABCD中，底面ABCD为矩形，PA⊥面ABCD，PA=PB=2．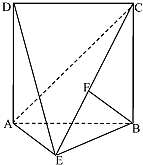
如图，四边形ABCD是边长为2的正方形，△ABE为等腰三角形，AE=BE，平面ABCD⊥平面ABE，动点F在校CE上，无论点F运动到何处时，总有BF⊥AE．