Question

已知点A是不等式组

x-3y+1≤0 x+y-3≤0 x≥1

所表示的平面区域内的一个动点，点B（-2，1），O为坐标原点，则|

OA

+

OB

|的最大值是

 

．

Answer 1

考点：简单线性规划

专题：不等式的解法及应用

分析：设A（x，y），z=|

OA

+

OB

|，求出z的大小，根据z的几何意义即可得到结论．

解答： 解：设A（x，y），则

OA

+

OB

=（-2，1）+（x，y）=（x-2，y+1），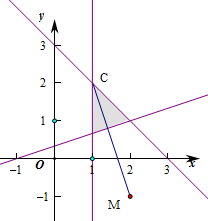
则|

OA

+

OB

|=

(x-2)2+(y+1)2

，
设z=|

OA

+

OB

|=

(x-2)2+(y+1)2

，则z的几何意义为点A到定点M（2，-1）的距离，
作出不等式组对应的平面区域如图：
由图象可知当点A位于C点时，CM的距离最大，
由

x=1 x+y-3=0

，解得

x=1 y=2

，即C（1，2），
则z=|

OA

+

OB

|=

(x-2)2+(y+1)2

=

1+9

=

10

，
故答案为：

10

点评：本题主要考查线性规划的应用，根据向量模的运算，利用数形结合是解决本题的关键．