题目内容
定义在R上的函数f（x）满足f（x+5）=f（x）．当-3＜x≤-1时，f（x）=x，当-1＜x≤2时，f（x）=（x-1）2，则f（1）+f（2）+f（3）+…+f（2014）= ．
考点：函数的周期性
专题：函数的性质及应用
分析：由f（x+5）=f（x）可知f（x）是以5为周期的函数，根据题目信息分别求得f（1），f（2），f（3），f（4），f（5）的值，再利用周期性即可得答案．
解答：
解：∵f（x+5）=f（x），
∴f（x）是以5为周期的函数，
∵-3＜x≤-1时，f（x）=x，
∴f（3）=f（-2）=-2，f（4）=f（-1）=-1，
又∵当-1＜x≤2时，f（x）=（x-1）2，
∴f（0）=1=f（5），f（1）=（1-1）2=0，
f（2）=（2-1）2=1，
∴f（1）+f（2）+f（3）+f（4）+f（5）=0+1-2-1+0=-2，
∴f（1）+f（2）+f（3）+…+f（2014）
=402×[f（1）+f（2）+f（3）+…+f（5）]+f（1）+f（2）+f（3）+f（4）
=402×（-2）+（-2）
=-806．
故答案为：-806．
∴f（x）是以5为周期的函数，
∵-3＜x≤-1时，f（x）=x，
∴f（3）=f（-2）=-2，f（4）=f（-1）=-1，
又∵当-1＜x≤2时，f（x）=（x-1）2，
∴f（0）=1=f（5），f（1）=（1-1）2=0，
f（2）=（2-1）2=1，
∴f（1）+f（2）+f（3）+f（4）+f（5）=0+1-2-1+0=-2，
∴f（1）+f（2）+f（3）+…+f（2014）
=402×[f（1）+f（2）+f（3）+…+f（5）]+f（1）+f（2）+f（3）+f（4）
=402×（-2）+（-2）
=-806．
故答案为：-806．
点评：本题考查了函数的周期性的应用，由题意求得f（1）+f（2）+f（3）+f（4）+f（5）的和是关键，考查转化与运算能力，属于中档题．
练习册系列答案
相关题目
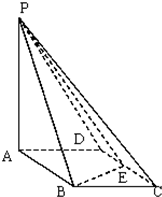如图所示，四棱锥P-ABCD的底面ABCD是边长为1的菱形，∠BCD=60°，E是CD的中点，PA⊥底面ABCD，PA=2．