题目内容
若不等式|x-4|-|x+1|≤a的解集为R，则a的取值范围是 ．
考点：绝对值不等式的解法
专题：不等式的解法及应用
分析：由条件利用绝对值三角不等式求得|x-4|-|x+1|的最大值为5，从而求得a的取值范围．
解答：
解：由于|x-4|-|x+1|≤|（x-4）-（x+1）|=5，故|x-4|-|x+1|的最大值为5，
再根据不等式|x-4|-|x+1|≤a的解集为R，可得a≥5，
故答案为：[5，+∞）．
再根据不等式|x-4|-|x+1|≤a的解集为R，可得a≥5，
故答案为：[5，+∞）．
点评：本题主要考查绝对值三角不等式，函数的恒成立问题，属于基础题．
练习册系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
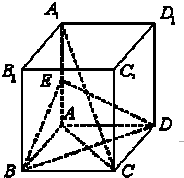如图，在正方体ABCD-A1B1C1D1中，E是AA1的中点．