题目内容
已知三棱柱ABC-A1B1C1的6个顶点都在球O的球面上，若AB=3cm，AC=4cm，AB⊥AC，AA1=12cm，则球O的表面积为 cm2．
考点：球的体积和表面积,球内接多面体
专题：计算题,空间位置关系与距离
分析：由于直三棱柱ABC-A1B1C1的底面ABC为直角三角形，我们可以把直三棱柱ABC-A1B1C1补成四棱柱，则四棱柱的体对角线是其外接球的直径，求出外接球的直径后，代入外接球的表面积公式，即可求出该三棱柱的外接球的表面积．
解答：
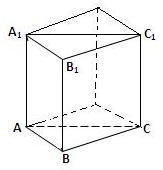解：由题意，三棱柱ABC-A1B1C1为直三棱柱ABC-A1B1C1，底面ABC为直角三角形，把直三棱柱ABC-A1B1C1补成四棱柱，
则四棱柱的体对角线是其外接球的直径，
所以外接球半径为
=13，
则三棱柱ABC-A1B1C1外接球的表面积是4πR2=169πcm2．
故答案为：169π．
解：由题意，三棱柱ABC-A1B1C1为直三棱柱ABC-A1B1C1，底面ABC为直角三角形，把直三棱柱ABC-A1B1C1补成四棱柱，则四棱柱的体对角线是其外接球的直径，
所以外接球半径为
| 1 |
| 2 |
| 32+42+122 |
则三棱柱ABC-A1B1C1外接球的表面积是4πR2=169πcm2．
故答案为：169π．
点评：本题考查球的体积和表面积，球的内接体问题，考查学生空间想象能力，是基础题．
练习册系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
已知tan（x+
）=
，0＜x＜
，则
=（ ）
| π |
| 4 |
| 12 |
| 5 |
| π |
| 4 |
| cos2x | ||
sin(
|
A、
| ||
B、
| ||
C、
| ||
D、-
|