题目内容
函数f(x)=
cos2x+
sinxcosx在[-
,
]的取值范围是 .
| 1 |
| 2 |
| ||
| 2 |
| π |
| 6 |
| π |
| 3 |
考点:三角函数中的恒等变换应用
专题:三角函数的求值
分析:利用二倍角公式和两角和公式对函数解析式化简整理,利用x的范围确定2x+
的范围,进而根据正弦函数的性质求得函数的值域.
| π |
| 6 |
解答:
解:f(x)=
cos2x+
sinxcosx=
+
sin2x=
sin(2x+
)+
,
∵x∈[-
,
],
∴2x+
∈[-
,
],
∴sin(2x+
)∈[-
,1],
∴f(x)max=
+
=
,f(x)min=-
+
=0,
∴函数f(x)的取值范围是[0,
],
故答案为:[0,
].
| 1 |
| 2 |
| ||
| 2 |
| cos2x+1 |
| 4 |
| ||
| 4 |
| 1 |
| 2 |
| π |
| 6 |
| 1 |
| 4 |
∵x∈[-
| π |
| 6 |
| π |
| 3 |
∴2x+
| π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
∴sin(2x+
| π |
| 6 |
| 1 |
| 2 |
∴f(x)max=
| 1 |
| 2 |
| 1 |
| 4 |
| 3 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
∴函数f(x)的取值范围是[0,
| 3 |
| 4 |
故答案为:[0,
| 3 |
| 4 |
点评:本题主要考查了三角函数恒等变换的应用,三角函数图象与性质.考查了学生对三角函数基础知识的理解和运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
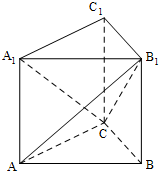 直三棱柱ABC-A1B1C1中,AC=BC=BB1=1,AB=
直三棱柱ABC-A1B1C1中,AC=BC=BB1=1,AB=
 如图是甲、乙两名同学在五场篮球比赛中得分情况的茎叶图,那么甲、乙两人和分的标准差s甲
如图是甲、乙两名同学在五场篮球比赛中得分情况的茎叶图,那么甲、乙两人和分的标准差s甲