题目内容
15．已知函数f（x）=$\left\{\begin{array}{l}{cos（1-{x}^{2}），x＜0}\\{-tan2x，x≥0}\end{array}\right.$，则f[f（$\frac{π}{8}$）]=（ ）| A． | -1 | B． | 0 | C． | 1 | D． | 2 |
分析 根据分段函数的表达式代入进行求解即可．
解答 解：∵f（$\frac{π}{8}$）=-tan（2×$\frac{π}{8}$）=-tan$\frac{π}{4}$=-1，
则f（-1）=cos[1-（-1）2]=cos0=1，
故选：C
点评 本题主要考查函数值的计算，根据分段函数的表达式利用代入法进行求解是解决本题的关键．
练习册系列答案
相关题目
6．等差数列{an}中，a3=5，S6=36，则S9=（ ）
| A． | 17 | B． | 19 | C． | 81 | D． | 100 |
3．已知函数f（x）和g（x）是两个定义在区间M上的函数，若对任意的x∈M，存在常数x0∈M，使得f（x）≥f（x0），g（x）≥g（x0），且f（x0）=g（x0），则称f（x）与g（x）在区间M上是“相似函数”．若f（x）=ax2+2（a-1）x-2lnx+b（a，b∈R）与g（x）=x+$\frac{1}{x}$在区间[$\frac{1}{2}$，2]上是“相似函数”，则a，b的值分别是（ ）
| A． | a=1，b=1 | B． | a=-1，b=-1 | C． | a=1，b=-1 | D． | a=-1，b=1 |
10．$\frac{i-1}{1+i}$=（ ）
| A． | -i | B． | i | C． | 1+i | D． | 1-i |
20．如图是一个空间几何体的三视图，则该几何体的侧面积是（ ）
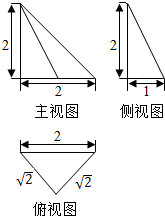
| A． | 3+$\sqrt{2}$+$\sqrt{3}$ | B． | $\frac{2}{3}$ | C． | 2+$\sqrt{2}$+$\sqrt{3}$ | D． | 5+$\sqrt{2}$ |
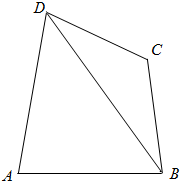如图，平面四边形ABCD中，CD=$\sqrt{3}$，∠CBD=30°，∠BCD=120°，AB=$\sqrt{5}$，AD=2$\sqrt{2}$，求