题目内容
20.如图是一个空间几何体的三视图,则该几何体的侧面积是( )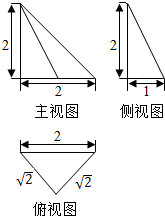
| A. | 3+$\sqrt{2}$+$\sqrt{3}$ | B. | $\frac{2}{3}$ | C. | 2+$\sqrt{2}$+$\sqrt{3}$ | D. | 5+$\sqrt{2}$ |
分析 由三视图知该几何体是三棱锥,且侧棱PA⊥底面ABC,CD⊥AB,利用勾股定理求出其它侧棱长,再利用直角三角形的面积公式求出侧面积.
解答 解:由三视图可知:该几何体是如图所示的三棱锥,
PA⊥底面ABC,CD⊥AB.
则PB=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$,PC=$\sqrt{{2}^{2}+(\sqrt{2})^{2}}$=$\sqrt{6}$,
所以PB2=PC2+BC2,即PC⊥PB
所以该几何体的侧面积S=$\frac{1}{2}×2×2+\frac{1}{2}×2×\sqrt{2}$+$\frac{1}{2}×\sqrt{2}×\sqrt{6}$
=2+$\sqrt{2}+\sqrt{3}$,
故选:C.
点评 本题考查了三棱锥的三视图,考查空间想象能力,三视图正确复原几何体是解题的关键,属于基础题.

练习册系列答案
相关题目
11.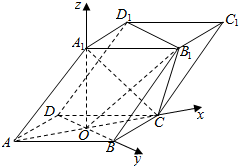 如图,四棱柱ABCD-A1B1C1D1的底面ABCD是正方形,O为底面中心,A1O⊥平面ABCD,AB=AA1=$\sqrt{2}$.平面OCB1的法向量$\overrightarrow{n}$=(x,y,z)为( )
如图,四棱柱ABCD-A1B1C1D1的底面ABCD是正方形,O为底面中心,A1O⊥平面ABCD,AB=AA1=$\sqrt{2}$.平面OCB1的法向量$\overrightarrow{n}$=(x,y,z)为( )
 如图,四棱柱ABCD-A1B1C1D1的底面ABCD是正方形,O为底面中心,A1O⊥平面ABCD,AB=AA1=$\sqrt{2}$.平面OCB1的法向量$\overrightarrow{n}$=(x,y,z)为( )
如图,四棱柱ABCD-A1B1C1D1的底面ABCD是正方形,O为底面中心,A1O⊥平面ABCD,AB=AA1=$\sqrt{2}$.平面OCB1的法向量$\overrightarrow{n}$=(x,y,z)为( )| A. | (0,1,1) | B. | (1,-1,1) | C. | (0,1,-1) | D. | (-1,-1,1) |
8.在定义域内既是奇函数又是减函数的是( )
| A. | y=$\frac{1}{x}$ | B. | y=-x+$\frac{1}{x}$ | ||
| C. | y=-x|x| | D. | y=$\left\{\begin{array}{l}{-x+1,x>0}\\{-x-1,x≤0}\end{array}\right.$ |
15.已知函数f(x)=$\left\{\begin{array}{l}{cos(1-{x}^{2}),x<0}\\{-tan2x,x≥0}\end{array}\right.$,则f[f($\frac{π}{8}$)]=( )
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
9.函数$y=sin(2x-\frac{π}{3})$与$y=cos(2x+\frac{2π}{3})$的图象关于直线x=a对称,则a可能是( )
| A. | $\frac{π}{24}$ | B. | $\frac{π}{12}$ | C. | $\frac{π}{8}$ | D. | $\frac{11π}{24}$ |
10.在复平面内,复数$\frac{2+i}{2i}$对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
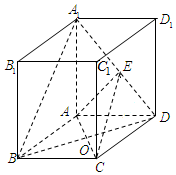 如图,四棱柱ABCD-A1B1C1D1中,底面四边形ABCD为菱形,∠ABC=60°,AA1=AC=2,A1B=A1D=2$\sqrt{2}$,点E在线段A1D上.
如图,四棱柱ABCD-A1B1C1D1中,底面四边形ABCD为菱形,∠ABC=60°,AA1=AC=2,A1B=A1D=2$\sqrt{2}$,点E在线段A1D上.