题目内容
计算:sin
-cos2
cosπ-
tan2
-cosπ+sin
= .
| π |
| 6 |
| π |
| 4 |
| 1 |
| 3 |
| π |
| 3 |
| π |
| 2 |
考点:三角函数的化简求值
专题:三角函数的求值
分析:直接利用特殊角的三角函数求值即可.
解答:
解:sin
-cos2
cosπ-
tan2
-cosπ+sin
=
-
×(-1)-
×3+1+1
=2.
故答案为:2.
| π |
| 6 |
| π |
| 4 |
| 1 |
| 3 |
| π |
| 3 |
| π |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
=2.
故答案为:2.
点评:本题考查三角函数的化简求值,特殊角的三角函数值的求法.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
 如图,AB是圆O的直径,C是圆O上的点.P是圆所在的面外一点.设Q为PA的中点,G为AOC的重心.求证:QG∥平面PBC.
如图,AB是圆O的直径,C是圆O上的点.P是圆所在的面外一点.设Q为PA的中点,G为AOC的重心.求证:QG∥平面PBC.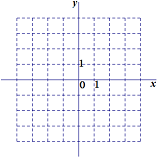 已知集合M={(x,y)|0≤y≤
已知集合M={(x,y)|0≤y≤