题目内容
已知f(x)是定义在R上的奇函数,且满足f(x+4)=-f(x),当x∈(0,2]时,f(x)=2x+4,则f(2015)=( )
| A、-2 | B、2 | C、-6 | D、6 |
考点:抽象函数及其应用
专题:函数的性质及应用
分析:由f(x+4)=-f(x)求得函数的周期为8,利用周期性和条件把f(2015)进行转化,直到求出函数值为止.
解答:
解:∵函数f(x)当x∈(0,2]时,f(x)=2x+4,∴f(1)=6,
由f(x+4)=-f(x)得,f(x+8)=-f(x+4)=f(x),即函数的周期为8,
∴f(2015)=f(251×8+7)=f(7)=f(7-8)=f(-1)=-f(1)
∵函数f(x)是定义在R上的奇函数,∴f(-1)=-f(1)=-6,
∴f(2015)=-6
故选:C.
由f(x+4)=-f(x)得,f(x+8)=-f(x+4)=f(x),即函数的周期为8,
∴f(2015)=f(251×8+7)=f(7)=f(7-8)=f(-1)=-f(1)
∵函数f(x)是定义在R上的奇函数,∴f(-1)=-f(1)=-6,
∴f(2015)=-6
故选:C.
点评:本题考查了函数周期性和奇偶性的应用,根据周期函数的性质和奇偶性对应的关系式,将所求的函数值对应自变量进行转化,转化到已知范围内求解,考查了转化思想.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若0<m<n<1,则( )
| A、3n<3m | ||||
| B、logm4<logn4 | ||||
| C、log5m<log5n | ||||
D、(
|
已知Sn=
+
+
+…+
,则当a=2时,S6=( )
| 1 |
| a |
| 2 |
| a2 |
| 3 |
| a3 |
| n |
| an |
A、
| ||
B、
| ||
| C、2 | ||
D、
|
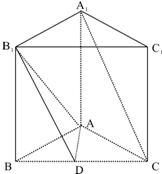 如图,底面是正三角形的直三棱柱ABC-A1B1C1中,D是BC的中点,AA1=AB=2.
如图,底面是正三角形的直三棱柱ABC-A1B1C1中,D是BC的中点,AA1=AB=2.