题目内容
用数字“1,2”组成一个四位数,则数字“1,2”都出现的四位数有 个.
考点:计数原理的应用
专题:排列组合
分析:本题需要分三类第一类,3个1,1个2,第二类,3个2,1个1,第三类,2个1,2个2,根据分类计数原理可得,或者利用列举法.
解答:
解:方法一:1,2”组成一个四位数,数字“1,2”都出现的共3类,
第一类,3个1,1个2,有3个1的排列顺序只有1种,把2插入到3个1所形成的4个间隔中,故有
=4个,
第二类,3个2,1个1,有3个2的排列顺序只有1种,把1插入到3个2所形成的4个间隔中,故有
=4个,
第三类,2个1,2个2,先排2个1只有一种,再把其中一个2插入到2个1只形成的3个间隔中,再把另一个2插入所形成的四个间隔中,2个2一样,故
•
=6,
根据分类计数原理,数字“1,2”都出现的四位数有4+4+6=14个
方法二,列举即可,1112,1121,1211,2111,1122,1212,1221,2121,2112,2211,2221,2212,2122,1222,共14个
故答案为14
第一类,3个1,1个2,有3个1的排列顺序只有1种,把2插入到3个1所形成的4个间隔中,故有
| A | 1 4 |
第二类,3个2,1个1,有3个2的排列顺序只有1种,把1插入到3个2所形成的4个间隔中,故有
| A | 1 4 |
第三类,2个1,2个2,先排2个1只有一种,再把其中一个2插入到2个1只形成的3个间隔中,再把另一个2插入所形成的四个间隔中,2个2一样,故
| 1 |
| 2 |
| A | 1 3 |
| A | 1 4 |
根据分类计数原理,数字“1,2”都出现的四位数有4+4+6=14个
方法二,列举即可,1112,1121,1211,2111,1122,1212,1221,2121,2112,2211,2221,2212,2122,1222,共14个
故答案为14
点评:本题主要考查了分类计数原理,如何分类是关键,属于基础题

练习册系列答案
相关题目
设Sn是等差数列{an}的前n项和,已知a5=9,S2=4,则a2=( )
| A、1 | B、2 | C、3 | D、5 |
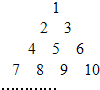 如图,自然数列按正三角形图顺序排列,如数9排在第4行第3个位置;设数2015排在第m行第n个位置,则m+n=
如图,自然数列按正三角形图顺序排列,如数9排在第4行第3个位置;设数2015排在第m行第n个位置,则m+n=