题目内容
对于函数f(x),若存在区间[m,n](m<n),使得f(x)在区间[m,n]上的值域为[λm,λn],则称f(x)为“λ倍函数”.
(Ⅰ)若函数f(x)=x3为“1倍函数”,求符合条件的区间[m,n].
(Ⅱ)若函数f(x)=k+
为“1倍函数”,求实数k的取值范围.
(Ⅰ)若函数f(x)=x3为“1倍函数”,求符合条件的区间[m,n].
(Ⅱ)若函数f(x)=k+
| x+2 |
考点:二次函数的性质
专题:函数的性质及应用
分析:(I)函数f(x)=x3为“1倍函数”,则存在区间[m,n],使得f(x)在区间[m,n]上的值域为[m,n],进而根据方程x3=x有三个解:-1,0,1,得到符合条件的区间[m,n].
(Ⅱ)若函数f(x)=k+
为“1倍函数”,则存在区间[m,n],使得f(x)在区间[m,n]上的值域为[m,n],即方程x=k+
在区间[-2,+∞)上有两个不同的解;也即方程x2-(2k+1)x+k2-2=0有两个都不小于k的不等根,由此构造关于k的不等式组,解不等式组得到实数k的取值范围.
(Ⅱ)若函数f(x)=k+
| x+2 |
| x+2 |
解答:
解:(I)函数f(x)=x3为“1倍函数”,
则存在区间[m,n],使得f(x)在区间[m,n]上的值域为[m,n],
又∵函数f(x)=x3为增函数,
故
,
由方程x3=x有三个解:-1,0,1,
故符合条件的区间可以为:[-1,0],[-1,1],[0,1].
(II)若函数f(x)=k+
为“1倍函数”,
则存在区间[m,n],使得f(x)在区间[m,n]上的值域为[m,n],
又∵f(x)=k+
在区间[-2,+∞)上为增函数,
故
.
即方程x=k+
在区间[-2,+∞)上有两个不同的解;
也即方程x2-(2k+1)x+k2-2=0有两个都不小于k的不等根,
令f(x)=x2-(2k+1)x+k2-2,
则
,
解得x∈(-
,-2],
故实数k的取值范围为:(-
,-2]
则存在区间[m,n],使得f(x)在区间[m,n]上的值域为[m,n],
又∵函数f(x)=x3为增函数,
故
|
由方程x3=x有三个解:-1,0,1,
故符合条件的区间可以为:[-1,0],[-1,1],[0,1].
(II)若函数f(x)=k+
| x+2 |
则存在区间[m,n],使得f(x)在区间[m,n]上的值域为[m,n],
又∵f(x)=k+
| x+2 |
故
|
即方程x=k+
| x+2 |
也即方程x2-(2k+1)x+k2-2=0有两个都不小于k的不等根,
令f(x)=x2-(2k+1)x+k2-2,
则
|
解得x∈(-
| 9 |
| 4 |
故实数k的取值范围为:(-
| 9 |
| 4 |
点评:本题考查的知识点是二次函数的性质,函数的单调性,方程根的个数,是函数与方程的综合应用,难度较大.

练习册系列答案
相关题目
 如图在四棱锥P-ABCD中,底面ABCD是边长为a的正方形,侧面PAD⊥底面ABCD,且PA=PD=
如图在四棱锥P-ABCD中,底面ABCD是边长为a的正方形,侧面PAD⊥底面ABCD,且PA=PD=
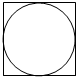 在图的正方形中随机撒一把芝麻,用随机模拟的方法估计圆周率π的值.如果撒了1000个芝麻,落在圆内的芝麻总数是781颗,那么这次模拟中π的估计值是
在图的正方形中随机撒一把芝麻,用随机模拟的方法估计圆周率π的值.如果撒了1000个芝麻,落在圆内的芝麻总数是781颗,那么这次模拟中π的估计值是