题目内容
 如图在四棱锥P-ABCD中,底面ABCD是边长为a的正方形,侧面PAD⊥底面ABCD,且PA=PD=
如图在四棱锥P-ABCD中,底面ABCD是边长为a的正方形,侧面PAD⊥底面ABCD,且PA=PD=
| ||
| 2 |
(1)求证:面PAB⊥平面PDC;
(2)求二面角B-PD-C的余弦值.
考点:用空间向量求平面间的夹角,平面与平面垂直的判定
专题:空间位置关系与距离,空间角
分析:(1)根据面面垂直的判定定理即可证明面PAB⊥平面PDC;
(2)建立空间直角坐标系,求出平面的法向量,利用向量法即可求二面角B-PD-C的余弦值.
(2)建立空间直角坐标系,求出平面的法向量,利用向量法即可求二面角B-PD-C的余弦值.
解答:
 解:(1)如图,取AD的中点O,连结OP,OF.
解:(1)如图,取AD的中点O,连结OP,OF.
∵PA=PD,∴PO⊥AD.
∵侧面PAD⊥底面ABCD,平面PAD∩平面ABCD=AD,
∴PO⊥平面ABCD,
而O,F分别为AD,BD的中点,∴OF∥AB,
又ABCD是正方形,故OF⊥AD.
∵PA=PD=
AD,∴PA⊥PD,OP=OA=
.
以O为原点,向量,为x,y,z轴建立空间直线坐标系,
则有A(
,0,0),F(0,
,0),D(-
,0,0),P(0,0,
),B(
,a,0),C(-
,a,0).
∵E为PC的中点,∴E(-
,
,
)
(1)∵
=(
,0,-
),=(0,-a,0)∴??=(,0,-)?(0,-a,0)=0,
∴
⊥
,从而PA⊥CD,又PA⊥PD,PD∩CD=D,
∴PA⊥平面PDC,而PA?平面PAB,
∴平面PAB⊥平面PDC.
(2)由(1)知平面PDC的法向量为
=(
,0,-
).
设平面PBD的法向量为
=(x,y,z).
∵=(,0,)?,=(-a,-a,0)
∴由
•
=0,
•
=0可得
取x=1,则y=-1,z=-1,故=(1,-1,-1)
∴cos<
,
>=
=
=
,
即二面角B-PD-C的余弦值为
.
 解:(1)如图,取AD的中点O,连结OP,OF.
解:(1)如图,取AD的中点O,连结OP,OF.∵PA=PD,∴PO⊥AD.
∵侧面PAD⊥底面ABCD,平面PAD∩平面ABCD=AD,
∴PO⊥平面ABCD,
而O,F分别为AD,BD的中点,∴OF∥AB,
又ABCD是正方形,故OF⊥AD.
∵PA=PD=
| ||
| 2 |
| a |
| 2 |
以O为原点,向量,为x,y,z轴建立空间直线坐标系,
则有A(
| a |
| 2 |
| a |
| 2 |
| a |
| 2 |
| a |
| 2 |
| a |
| 2 |
| a |
| 2 |
∵E为PC的中点,∴E(-
| a |
| 4 |
| a |
| 2 |
| a |
| 4 |
(1)∵
| PA |
| a |
| 2 |
| a |
| 2 |
∴
| PA |
| CD |
∴PA⊥平面PDC,而PA?平面PAB,
∴平面PAB⊥平面PDC.
(2)由(1)知平面PDC的法向量为
| PA |
| a |
| 2 |
| a |
| 2 |
设平面PBD的法向量为
| n |
∵=(,0,)?,=(-a,-a,0)
∴由
| n |
| DP |
| n |
| BD |
取x=1,则y=-1,z=-1,故=(1,-1,-1)
∴cos<
| n |
| PA |
| ||||
|
|
| a | ||||||
|
| ||
| 3 |
即二面角B-PD-C的余弦值为
| ||
| 3 |
点评:本题主要考查平面和平面垂直的判定以及空间二面角的计算,建立空间直角坐标系,利用向量法是解决本题的关键.

练习册系列答案
相关题目
 某少数民族的刺绣有着悠久的历史,如图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这些图案都由小三角形构成,小三角形数越多刺绣越漂亮,现按同样的规律刺绣(小三角形的摆放规律相同),设第n个图形包含f(n)个小三角形.由图形知f(1)=1,f(2)=3,f(3)=6
某少数民族的刺绣有着悠久的历史,如图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这些图案都由小三角形构成,小三角形数越多刺绣越漂亮,现按同样的规律刺绣(小三角形的摆放规律相同),设第n个图形包含f(n)个小三角形.由图形知f(1)=1,f(2)=3,f(3)=6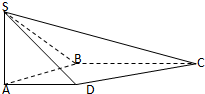 如图,在四棱锥S-ABCD中,SA⊥平面ABCD,底面ABCD为直角梯形,AD∥BC,∠ABC=90°,SA=AB=1,
如图,在四棱锥S-ABCD中,SA⊥平面ABCD,底面ABCD为直角梯形,AD∥BC,∠ABC=90°,SA=AB=1,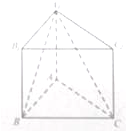 如图,在直三棱柱ABC-A1B1C1中,AB=2,AC=AA1=2
如图,在直三棱柱ABC-A1B1C1中,AB=2,AC=AA1=2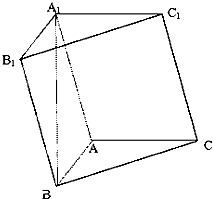 在三棱柱ABC-A1B1C1中,AB⊥AC,AB=AC=A1B=2,顶点A1在底面ABC上的射影恰好为点B.
在三棱柱ABC-A1B1C1中,AB⊥AC,AB=AC=A1B=2,顶点A1在底面ABC上的射影恰好为点B.