题目内容
在三棱锥P-ABC中,PA⊥底面ABC,AC⊥BC,PA=AC=BC,则直线PC与AB所成角的大小是 .
考点:异面直线及其所成的角
专题:计算题,空间角
分析:取PA中点E,PB中点F,BC中点G,连接AG,由三角形中位线定理可得∠EFG(或其补角)就是异面直线AB与PC所成的角.然后在Rt△AEG中算出EG的长,用中位线定理得到EF=FG=
,最后在△EFG中用余弦定理算出∠EFG=120°,即得异面直线AB与PC所成角的大小.
| 2 |
解答:
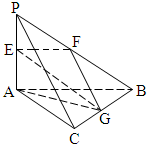 解:取PA中点E,PB中点F,BC中点G,连接EF,FG,EG,
解:取PA中点E,PB中点F,BC中点G,连接EF,FG,EG,
∵EF、FG分别是△PAB、△PBC的中位线
∴EF∥AB,FG∥PC,
因此,∠EFG(或其补角)就是异面直线AB与PC所成的角.
连接AG,则Rt△AEG中,AG=
=
,
EG=
=
,
又∵AB=PC=2
,∴EF=FG=
.
由此可得,在△EFG中,cos∠EFG=
=-
结合∠EFG是三角形内角,可得∠EFG=120°.
综上所述,可得异面直线AB与PC所成角的大小为60°.
故答案为:60°.
 解:取PA中点E,PB中点F,BC中点G,连接EF,FG,EG,
解:取PA中点E,PB中点F,BC中点G,连接EF,FG,EG,∵EF、FG分别是△PAB、△PBC的中位线
∴EF∥AB,FG∥PC,
因此,∠EFG(或其补角)就是异面直线AB与PC所成的角.
连接AG,则Rt△AEG中,AG=
| AC2+CG2 |
| 5 |
EG=
| EA2+AG2 |
| 6 |
又∵AB=PC=2
| 2 |
| 2 |
由此可得,在△EFG中,cos∠EFG=
| EF2+FG2-EG2 |
| 2EF•FG |
| 1 |
| 2 |
结合∠EFG是三角形内角,可得∠EFG=120°.
综上所述,可得异面直线AB与PC所成角的大小为60°.
故答案为:60°.
点评:本题给出一条侧棱垂直于底面的三棱锥,求异面直线所成角,着重考查了异面直线及其所成的角及其求法等知识,属于基础题.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
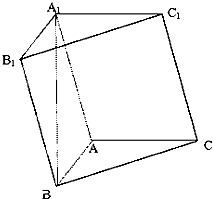 在三棱柱ABC-A1B1C1中,AB⊥AC,AB=AC=A1B=2,顶点A1在底面ABC上的射影恰好为点B.
在三棱柱ABC-A1B1C1中,AB⊥AC,AB=AC=A1B=2,顶点A1在底面ABC上的射影恰好为点B.