题目内容
16.△ABC的内角A,B,C的对边分别为a,b,c,已知bcosC=(2a-c)cosB.(Ⅰ)求B;
(Ⅱ)若$b=\sqrt{7}$,△ABC的面积为$\frac{{3\sqrt{3}}}{2}$,求△ABC的周长.
分析 (Ⅰ)由已知及正弦定理,两角和的正弦函数公式,三角形内角和定理,诱导公式可求sinA=2sinAcosB,结合sinA≠0,可求cosB的值,利用特殊角的三角函数值即可得解B的值.
(Ⅱ)由已知及三角形面积公式可求ac=6,进而利用余弦定理可求a+c的值,从而可求周长.
解答 (本题满分为12分)
解:(Ⅰ)由已知及正弦定理得sinBcosC=(2sinA-sinC)•cosB=2sinAcosB-sinCcosB.…(2分)
可得:sinBcosC+sinCcosB=2sinAcosB,
可得:sin(B+C)=2sinAcosB,故sinA=2sinAcosB,
因为,sinA≠0,
所以$cosB=\frac{1}{2}$,$B=\frac{π}{3}$.…(6分)
(Ⅱ)由已知,$\frac{1}{2}acsinB=\frac{{3\sqrt{3}}}{2}$,
又$B=\frac{π}{3}$,所以ac=6.…(8分)
由已知及余弦定理得,a2+c2-2accosB=7,
故a2+c2=13.…(10分)
从而(a+c)2=25,可得:a+c=5.
所以△ABC的周长为$5+\sqrt{7}$.…(12分)
点评 本题主要考查了正弦定理,两角和的正弦函数公式,三角形内角和定理,诱导公式,特殊角的三角函数值,三角形面积公式,余弦定理在解三角形中的综合应用,考查了转化思想,属于基础题.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
6.正方体的棱长为2$\sqrt{3}$,顶点都在同一球面上,则该球的表面积为( )
| A. | 36π | B. | 72π | C. | 288π | D. | 144π |
11.某校校庆期间,大会秘书团计划从包括甲、乙两人在内的七名老师中随机选择4名参加志愿者服务工作,根据工作特点要求甲、乙两人中至少有1人参加,则甲、乙都被选中且列队服务时不相邻的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{4}$ |
1.若集合M={x|(x-1)(x-4)=0},N={x|(x+1)(x-3)<0},则M∩N=( )
| A. | ∅ | B. | {1} | C. | {4} | D. | {1,4} |
5.某租车公司给出的财务报表如下:
有投资者在研究上述报表时,发现租车公司有空驶情况,并给出空驶率的计算公式为$T=\frac{t-ak}{ak}•100%$.
(1)分别计算2014,2015年该公司的空驶率的值(精确到0.01%);
(2)2016年该公司加强了流程管理,利用租车软件,降低了空驶率并提高了平均每单里程,核算截止到11月30日,空驶率在2015年的基础上降低了20个百分点,问2016年前11个月的平均每单油费和平均每单里程分别为多少?(分别精确到0.01元和0.01公里)
 | 1014年(1-12月) | 1015年(1-12月) | 1016年(1-11月) |
| 接单量(单) | 14463272 | 40125125 | 50331996 |
| 油费(元) | 214301962 | 591305364 | 653214963 |
| 平均每单油费t(元) | 14.82 | 14.49 | |
| 平均每单里程k(公里) | 15 | 15 | |
| 每公里油耗a(元) | 0.7 | 0.7 | 0.7 |
(1)分别计算2014,2015年该公司的空驶率的值(精确到0.01%);
(2)2016年该公司加强了流程管理,利用租车软件,降低了空驶率并提高了平均每单里程,核算截止到11月30日,空驶率在2015年的基础上降低了20个百分点,问2016年前11个月的平均每单油费和平均每单里程分别为多少?(分别精确到0.01元和0.01公里)
6.在空间直角坐标系O-xyz中.正四面体P-ABC的顶点A,B分别在x轴,y轴上移动.若该正四面体的棱长是2,则|OP|的取值范围是( )
| A. | [$\sqrt{3}$-1,$\sqrt{3}$+1] | B. | [1,3] | C. | [$\sqrt{3}$-1,2] | D. | [1,$\sqrt{3}$+1] |
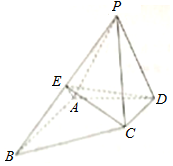 如图,四棱锥P-ABCD中,△PAD为正三角形,AB∥CD,AB=2CD,∠BAD=90°,PA⊥CD,E为棱PB的中点
如图,四棱锥P-ABCD中,△PAD为正三角形,AB∥CD,AB=2CD,∠BAD=90°,PA⊥CD,E为棱PB的中点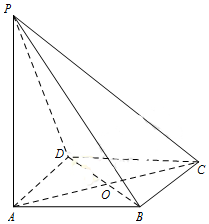 如图,ABCD是菱形,PA⊥平面ABCD,PA=AD=2,∠BAD=60°.
如图,ABCD是菱形,PA⊥平面ABCD,PA=AD=2,∠BAD=60°.