题目内容
6.在空间直角坐标系O-xyz中.正四面体P-ABC的顶点A,B分别在x轴,y轴上移动.若该正四面体的棱长是2,则|OP|的取值范围是( )| A. | [$\sqrt{3}$-1,$\sqrt{3}$+1] | B. | [1,3] | C. | [$\sqrt{3}$-1,2] | D. | [1,$\sqrt{3}$+1] |
分析 根据题意画出图形,结合图形,固定正四面体P-ABC的位置,则原点O在以AB为直径的球面上运动,
原点O到点P的最近距离等于PM减去球的半径,最大距离是PM加上球的半径.
解答 解: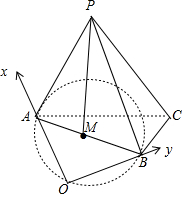
如图所示,若固定正四面体P-ABC的位置,则原点O在以AB为直径的球面上运动,
设AB的中点为M,则PM=$\sqrt{{2}^{2}{-1}^{2}}$=$\sqrt{3}$;
所以原点O到点P的最近距离等于PM减去球M的半径,
最大距离是PM加上球M的半径;
所以$\sqrt{3}$-1≤|OP|≤$\sqrt{3}$+1,
即|OP|的取值范围是[$\sqrt{3}$-1,$\sqrt{3}$+1].
故选:A.
点评 本题主要考查了点到直线以及点到平面的距离与应用问题,也考查了数形结合思想的应用问题,是综合题.

练习册系列答案
相关题目
14.复数$z=\frac{i}{1-i}$的共轭复数的模为( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | 1 | D. | 2 |
11.若集合A={0,1,2,4},B={1,2,3},则A∩B=( )
| A. | {0,1,2,3,4} | B. | {0,1} | C. | {0,1,4} | D. | {1,2} |
16.下列命题中不正确的是( )
| A. | 如果平面α⊥平面 γ,平面β⊥平面 γ,α∩β=l,那么l⊥γ | |
| B. | 如果平面α⊥平面 β,那么平面α内一定存在直线平行于平面β | |
| C. | 如果平面α不垂直于平面β,那么平面α内一定不存在直线垂直于平面β | |
| D. | 如果平面α⊥平面 β,过α内任意一点作交线的垂线,那么此垂线必垂直于β |