题目内容
11.某校校庆期间,大会秘书团计划从包括甲、乙两人在内的七名老师中随机选择4名参加志愿者服务工作,根据工作特点要求甲、乙两人中至少有1人参加,则甲、乙都被选中且列队服务时不相邻的概率为( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{4}$ |
分析 先求出基本事件总数n=(${C}_{2}^{1}{C}_{5}^{3}$+${C}_{2}^{2}{C}_{5}^{2}$)${A}_{4}^{4}$=720,再求出甲、乙都被选中且列队服务时不相邻包含的基本事件个数m=${C}_{2}^{2}{C}_{5}^{2}{A}_{2}^{2}{A}_{3}^{2}$=120,由此能求出甲、乙都被选中且列队服务时不相邻的概率.
解答 解:从包括甲、乙两人在内的七名老师中随机选择4名参加志愿者服务工作,
根据工作特点要求甲、乙两人中至少有1人参加,且列队服务,
基本事件总数n=(${C}_{2}^{1}{C}_{5}^{3}$+${C}_{2}^{2}{C}_{5}^{2}$)${A}_{4}^{4}$=720,
甲、乙都被选中且列队服务时不相邻包含的基本事件个数m=${C}_{2}^{2}{C}_{5}^{2}{A}_{2}^{2}{A}_{3}^{2}$=120,
甲、乙都被选中且列队服务时不相邻的概率p=$\frac{m}{n}=\frac{120}{720}$=$\frac{1}{6}$.
故选:C.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意等可能事件概率计算公式的合理运用.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
2.某几何体的三视图如图所示,则该几何体外接球的表面积为( )
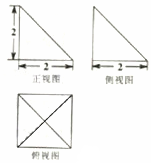

| A. | 4π | B. | 12π | C. | 48π | D. | 6$\sqrt{3}$π |
19.要得到函数$y=cos({2x-\frac{π}{3}})$的图象,只需将函数y=sin2x的图象( )
| A. | 向左平移$\frac{π}{12}$个单位 | B. | 向右平移$\frac{π}{12}$个单位 | ||
| C. | 向左平移$\frac{π}{6}$个单位 | D. | 向右平移$\frac{π}{6}$个单位 |
6.m,n表示两条不同直线,α,β,γ表示平面,下列说法正确的个数是( )
①若α∩β=m,α∩γ=n,且m∥n,则β∥γ;
②若m,n相交且都在α,β外,m∥α,m∥β,n∥α,n∥β,则α∥β;
③若α∩β=l,m∥α,m∥β,n∥α,n∥β,则m∥n;
④若m∥α,n∥α,则m∥n.
①若α∩β=m,α∩γ=n,且m∥n,则β∥γ;
②若m,n相交且都在α,β外,m∥α,m∥β,n∥α,n∥β,则α∥β;
③若α∩β=l,m∥α,m∥β,n∥α,n∥β,则m∥n;
④若m∥α,n∥α,则m∥n.
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
3.设a=log310,b=log37,则3a-b=( )
| A. | $\frac{10}{49}$ | B. | $\frac{49}{10}$ | C. | $\frac{7}{10}$ | D. | $\frac{10}{7}$ |
20.设x,y∈R,则“|x|+|y|>1”的一个充分条件是( )
| A. | |x|≥1 | B. | |x+y|≥1 | C. | y≤-2 | D. | $|x|≥\frac{1}{2}$且$|y|≥\frac{1}{2}$ |